POSTS
Breaking News: Dramatic changes in U.S. political landscape.

Breaking News: Dramatic changes in U.S. political landscape.It will shortly be announced that President Trump will appoint his daughter Ivanka to president of the World Bank, batman as Chief International Troubleshooter, and spiderman as ambassador to the European Union. He himself will take over the role as Calif of Bagdad, as miraculously predicted 1000 years ago in the Tales of 1001 Nights. He will of course stay on as President of the U.S. He declared that he wants to get out of the sand and death of Syria, the oil-rich Iraq being a much better investment. Let the bastards pay for all America has done for them. – Ivanka is uniquely qualified for her new role, after all she run a successful womens’ wear business for many years before getting into higher politics, Batman knows how to get into trouble and out, and Spiderman will use his webs to make the countries of the EU stick together, a dear dream the President has held for many years.
For further details see: https://krohde.wordpress.com/2019/02/03/breaking-news-important-changes-in-us-political-landscape-the-physiognomy-of-evil-die-physiognomie-des-ublen/
All illustrations my originals. – This work is licensed under a Creative Commons Attribution-Share Alike 3.0 Licens
Advertisements
Occasionally, some of your visitors may see an advertisement here,
as well as a Privacy & Cookies banner at the bottom of the page.
You can hide ads completely by upgrading to one of our paid plans.
The doomsday clock and Trump’s City on the Hill/Die Doomsday-Uhr und Trumps Stadt auf dem Hügel

Fire and fury, Feuer und Wut
My new bilingual post examines whether Trump’s politics is an aberration or a continuation of the politics of earlier presidents/ Mein neuer bilingualer Post untersucht die Frage, ob Trumps Politik eine Fortsetzung früherer Politik oder aber eine Fehlentwicklung ist.
See here/siehe hier:
The Doomsday Clock and Trump’s city on the hill/Die Doomsday Uhr und Trumps Stadt auf dem Hügel
Offener Brief an ‘Deutsche Welle’: Kultur im ‘Tag’
Ein offener Brief an die ‘Deutsche Welle’
Vor einigen Jahren zeigte die Neue Nationalgallerie Berlin eine Ausstellung, in der Gemälde aus der damaligen DDR Gemälden aus der Bundesrepublik gegenüber gestellt wurden. Aus dem Westen fast nur (oder nur) Abstraktes, durchweg Schablone und zweitklassig, aus der DDR vorwiegend (oder nur) figürlich, sehr interessant und zum Teil ausgezeichnet. Ich habe nichts gegen abstrakte Kunst, im Gegenteil , ich halte Klee, Miro, Kandinsky, um nur einige zu nennen, für grosse Künstler, aber was hier zu sehen war, ist in meinen Augen ziemlicher Mist. Erst später erfuhr ich, dass die CIA die Kunstentwicklung im Westen finanziell steuerte, durch den ‘Kongress für kulturelle Freiheit https://www.wikiwand.com/de/Kongress_f%C3%BCr_kulturelle_Freiheit. Warum wohl? Es erklärt auf jeden Fall, warum “Abstrakt” sich so plötzlich ausbreitetete.
Ich notierte mir über mehrere Tage, was in der Kultursektion des ‘Tages’ (erst Hälfte) über einige Tage präsentiert wurde: Woody Allen Sex Skandal, Angebliche Plagiate eines Schlagers, Amerikanische Popart (zwei Ausstellungen in Baden-Baden und Köln (?), ein in New York lebender Pianist, Hollywood Granny Awards, Film Phantom Thread (der seidene Faden), Film Black Panther, beide USA, Karneval in der Lagunenstadt (Venedig), letzteres die einzige nicht-amerikanische und sehr gute Ausnahme. Es ist mir zwar klar, dass der Kongress für kulturelle Freiheit schon vor vielen Jahren aufgelöst wurde, aber man bekommt den Eindruck, dass die Deutsche Welle, die ja wohl auch deutsche “Kultur” propagieren sollte, in erster Linie ein Ableger der amerikanischen Kulturindustrie ist.
Für wen sind solche Sendungen eigentlich gedacht? Hat die Deutsche Welle auch nur eine annähernde Ahnung von der Zusammensetzung ihrer Zuhörerschaft? Ich kann mir nicht vorstellen dass hier in Australien besonderes Interesse an der von der D.W. ausgestrahlten ‘Kultur ‘ besteht, sowieso schon übersättigt mit Hollywood usw. im lokalen Fernsehen.
Und es liegt sicherlich nicht daran, dass kein Interesse an deutscher Kultur, besteht. Im Gegenteil, vor allem deutsche Musik (Symphonie, Kammerkonzerte, Oper) sind unter den gebildeten Schichten ‘populär’, aber auch Theater. Gross und Klein von Botho Strauss, Stücke und Songs von Kurt Weil/Bertolt Brecht, zum Beispiel, waren Hits.
Ich betone, dass sich meine Bemerkungen ausschliesslich auf die jeweils erste Hälfte des ‘Tages’ beziehen, die zweite wird hier in Australien nicht ausgestrahlt. Vielleicht sind all die guten Sachen in der zweiten Hälfte.
Um mit etwas Positivem zu schliessen: Die Interviews mit Thomas Spahn, die Reportagen über die Türkei von Julia Hahn, und die Sendungen von Jens Olesen sind durchweg sehr gut, was nicht heissen soll, dass es nicht auch anderes Gutes gibt.
——————-
Ich lebte als Jugendlicher in der Ostzone und war (und bin) keineswegs ein Bewunderer des sozialistischen Realismus. Siehe hier:
Trump’s Pick: Secretary of State Rex Tillerson, CEO of Exxon Mobil and Prominent Climate Change Denier
The Center for Media and Democracy’s PR Watch has published a detailed article on the activities of Rex Tillerson while CEO of Exxon Mobil:
Rex Tillerson and Exxon Spent Big on Climate Change Denial while Misleading Public, Evidence Shows
Quotes:
‘Exxon has used “ALEC’s charitable status to fuel its disinformation campaign on climate change, so taxpayers are literally paying Exxon to lie to them’
‘ Notably, Tillerson’s block of shareholders held off a voluntary measure sought by minority stockholders from the Rockefeller family to significantly expand Exxon’s investment in alternative energy sources.’
Rex Tillerson, if confirmed, will be one of the most influential members of Trump’s cabinet, for example responsible for negotiations with President Putin and his cabinet on oil and gas exploration in the Arctic, recently banned by President Obama in the American sphere. Could an agreement with Russia become a way of circumventing this ban? Of course there are many other issues involved. How can the conflicting interests of Trump as a business man and president of the US be disentangled? Nobody will seriously believe that handing over control of his businesses to family members will guarantee that political decisions will not be influenced by how they might affect his profits. So far (during the election campaign) , Trump could not even be persuaded to reveal what taxes he had to pay, i.e., what his profits from his various businesses were. Was the appointment of Rex Tillerson as Secretary of State influenced by Trump’s business interests ?
See also here:
Center for Media and Democracy and Common Cause file extensive new evidence in whistleblower tax fraud case against ALEC
http://www.exposedbycmd.org/2016/10/06/exxon-alec-running-illegal-lobbying-scheme-irs-complaint/
Climate Change and the Future of Mankind: Donald Trump and his Team
The last section of the book edited by me: The Balance of Nature and Human Impact, Cambridge University Press 2013, http://www.cambridge.org/9781107019614 , ends as follows:
‘………. climate change is just one of the dangers facing nature and
mankind; others include over-exploitation of resources caused by population growth
and over-consumption, habitat destruction such as deforestation, pollution, and invasive
species. With regard to climate change, we conclude with a quote from an
Amazon “ description” of the important book by the American physicist and climate
expert Joseph Romm (2006), which suggests that everything is not yet lost. There is
hope if we do something now. Because of the prominent role of the USA as an
economic and scientifi c power, a leading role will have to be played by that country,
but countries such as Australia with its enormous coal and gas reserves must play their
role as well.
“ Global warming is the story of the twenty-first century. It is the most serious issue
facing the future of humankind, but American energy and environmental policy is
driving the whole world down a path toward global catastrophe. According to Joseph
Romm, we have ten years, at most, to start making sharp cuts to our greenhouse gas
emissions, or we will face disastrous consequences. The good news, he writes, is that
there is something we can do – but only if the leadership of the U.S. government acts
immediately and asserts its influence on the rest of the world.”’
(Citation from Romm, J. N. (2006). Hell and High Water: Global Warming–the Solution and the Politics–and What We Should Do. New York: William Morrow.)
President Obama had taken steps to address some of the issues related to climate change, although he was restricted in what he could do by the obstruction of the Congress. What can we expect from the team assembled by the President-elect Donald Trump? Paul McGeough, in the Sydney Morning Herald December 17-18, has given an overview of the team, yet to be confirmed by the Senate (‘All The President’s Men (and women)’: Two retired generals head Defense and Homeland Security, and a third will be National Security Advisor. All three have fairly right-wing views, in particular the third one, Michael Flynn, with respect to Iran. Secretary of State is the ‘outgoing chairman and stockholder of Exxon Mobil’, a ‘climate change sceptic’, Chief Strategist the ‘white nationalist and former chairman of inflammatory far-right propaganda platform Breithart’, compared with which even the Murdoch run Fox News is moderate; CIA Director is ‘outspoken in favour of CIA’s use of torture and against Iran nuclear deal’; Attorney General is a former state attorney general who ‘failed confirmation as a judge in 1986 due to alleged racist comments’; Labor is a fast food chain executive, opponent of minimum wage laws and Obamacare’; Energy is a climate change sceptic; Health and Human Services is is a strong opponent of Obamacare, ‘womens’ health programs and abortion’; Education is a billionairess who is a ‘strong advocate of charter schools and voucher funding for school choice’; Environmental Protection Agency is a ‘climate change denier…close to fossil fuel industry’; etc.
According to McGeough, ‘the team is mostly wealthy-dominated by billionaires and megamillionaires. By one calculation, the combined wealth of Trump’s 17 picks to date, more than $9.5 billion, is greater than the combined wealth of the 43 million least wealthy households in the country…’
What can we expect? Trump has repeatedly emphasized that he would reduce corporate tax and that Obamacare would be abolished or strongly modified. He has used aggressive language against Iran and China, will send large numbers of Mexicans back and build a wall (partly now to be replaced by fences, apparently, and to be paid by Mexico), and has promised to make America strong again, also by building up its military. Concerning climate change, his and his team’s past histories suggest that all the progress made under Obama will very likely be reversed. He even went so far as to proclaim that the USA would leave the Paris climate change agreement. Some reports claim that the NSA will have to concentrate on space activities and stop monitoring activities of climate change on Earth. Some NSA climate scientists feel so threatened that they have begun to make backups of climate data on their private computers. NASA appears to have the largest and most important such data base of any country; without it predictions of climate change would become almost impossible. All this may sound ridiculously insane, but in Australia -for example- there also have been attempts (only partially successful) by the more extreme wing of the right-wing government to restrict climate work by the CSIRO, the Australian national research organization, which has been at the forefront of climate research in Antarctica.
What does all this mean for our future? Accumulating research data, for example those on melting of ice sheets in Greenland and the Antarctic and its effects on sea level rises, show how urgent research on the threats posed by climate change are. We must know how great and how fast the changes will be, if we want to take effective measures to guarantee the survival of mankind. One should never give up hope, but the (not yet confirmed) composition of the new government of the US does not look good, to phrase it mildly.
The Future of Our Policy on Iran. Beware a second Iraq!
In the American election campaign, Donald Trump repeatedly declared he would tear up the nuclear deal with Iran.
The former Premier of New South Wales and Foreign Minister of Australia, Bob Carr, has this to say about Trump’s policy on Iran, in an article in the Sydney Morning Herald December 8, titled “As Trump casts around for a fight or two, we should quietly ease off military ties” (with America):
According to Carr, Peter Jennings of the Australian Strategic Policy Institute believes ‘now is the time or Australia to further integrate its armed forces with America’s’, ‘now we have an opportunity to modernise the alliance in ways that will meet higher US expectations“.
Bob Carr argues against this:
“In this same spirit of going forth to find unnecessary fights the Trump transition team is examining new US sanctions against Iran unrelated to Iran’s now-halted nuclear weapons development. Trump may be accepting he cannot tear up the Iran deal on day one as he promised. The deal is not just between America and Iran. It’s between eight parties – including the European Union and Russia. “He can’t tear it up,” one American has told me. “The deal is laminated.”
Kim Beazley as ambassador in Washington found that Republican senators on record opposing the Iran deal were quietly hoping it would be approved. They did not want to inherit a problem from hell: an Iran unrestrained in reaching a nuclear bomb within three months.
Members of the Obama administration fear Trump, unable to “tear up” the Iran agreement, will apply extra sanctions on other subjects – human rights or the behaviour of its vessels in the Gulf – until Iranian hardliners take command and themselves “tear up” the agreement.
General Michael Flynn is Trump’s national security adviser, very likely to be more powerful than the eventual secretary of state.
This week The New York Times discovered that in the 2012 Benghazi crisis, produced by a jihadist assault on the US consulate, he alone insisted that Iran was behind the attack.
To this day not even the Israel lobby or hardline Republicans in the Senate have been able to produce evidence that Iran was behind Benghazi.
The New York Times said, “For weeks, he pushed analysts for evidence that the attack might have had a state sponsor – sometimes shouting at them when they didn’t come to the conclusions he wanted”.
His behaviour had a distinct resemblance to the Bush administration’s determination to invent a case that Saddam possessed weapons of mass destruction.”
———–
At about the same time, the British Prime Minister Theresa May declared in a speech to Gulf State leaders that Britain would support the States against Iran.
“It follows a speech by Foreign Secretary Boris Johnson in which he sought to align British rhetoric more closely with that of the incoming administration of US President-elect Donald Trump.”
BBC News http://www.bbc.com/news/uk-politics-38227680
Extract:
“Speaking at summit of the Gulf Co-operation Council – comprising Saudi Arabia, Kuwait, the United Arab Emirates, Oman, Qatar and Bahrain – Mrs May also said the UK wanted to “make a more permanent and more enduring commitment to the long-term security of the Gulf” and would invest more than £3bn in defence spending in the region over the next 10 years.
“Gulf security is our security,” she said.
“Extremists plotting terror attacks here, in this region, are not only targeting the Gulf but, as we have seen, targeting the streets of Europe, too.
“Whether we’re confronting the terrorism of al-Qaeda, or the murderous barbarity of [so-called Islamic State], no country is a more committed partner for you in this fight than the UK.”
Mrs May said she was determined to build further on the trade and investment relationship between the Gulf and the UK.
“Just as Gulf security is our security, so your prosperity is also our prosperity. Already the Gulf is a special market for the UK.”
She said that last year trade between the UK and the Gulf was worth more than £30bn and, at the same time, Gulf investment in the UK was helping to regenerate cities from Aberdeen to Teeside and Manchester to London.”
“She alleged that Iran’s activities include:
- Sending fighters including the Islamic Revolutionary Guards Corps ‘Qods Force to Syria to shore up President Bashar al-Assad
- Providing support to the Houthi rebel movement in Yemen, and so working against the interests of the international community in bringing about peace and stability in the country
- Undermining stability in Lebanon and Iraq”
————–
Conveniently forgotten is that Iran was invited by the legitimate government of Syria to help it in its fight against what it believes to be terrorists including AlQaida and IS, and it is in Iraq by invitation of the Iraqi government, fighting against IS. It supports Hezbollah in Lebanon and the Houthis in Yemen, both of which as Shiites feel threatened by the Sunni alliance led by Saudi Arabia, which has bombarded the Houthis resulting in thousands of civilian casualties over many months. Who then are the terrorists in the Middle East, and is Britain’s policy there predominantly, if not entirely, determined by its economic interests? And who is behind the extremists such as Al Qaida and IS? Certainly not Iran!
I believe that Bob Carr deserves our full support. Likewise, Europe should not – like Theresa May does – try to ingratiate itself with the US, but follow a line that guarantees stability and peace. Future generations would certainly not understand support for a belligerent development which may have disastrous consequences (see Iraq).
Mainstream and social media in politics
The recent elections in the US have shown that outcomes of elections are to a great extent determined by who uses the media (now importantly including the social media like facebook) most cleverly and ruthlessly. Not the message but how it is presented to the people is important. Even lies will sway the electorate as long as they are presented convincingly. One could go further and say ‘exciting’ (i.e. totally unexpected) lies lend themselves more easily to swaying the public than the ‘boring’ truth. Tell the electorate that President Obama is not really American but was born in Africa or Indonesia, or that the Pope backs Trump during the election, and many will fall for it, not bothering to check the facts. Interesting in this context that the Australian public broadcaster ABC, after appointment of a new boss of ABC by the rightwing government, plans to scrap a program ‘Fact Check,’ in which statements by prominent politicians are checked for their truth. – Various commentators have drawn attention to this phenomenon in the context of the recent American elections, concentrating on social media (facebook, twitter). However, the public has been misled for a very long time by the mainstream media, which is particularly clear with regard to the politics of climate change. I and some coauthors have discussed this in the section “the societal role in combating overexploitation and climate change: information policy” in Klaus Rohde editor: The Balance of Nature and Human Impact. Cambridge University Press 2013. I have also discussed it in a post
On the way to fascism? Climate change and media concentration
In Australia, about two thirds of the printed media are controlled by Murdoch, who also controls much of the mainstream media in Great Britain and USA (to mention only Fox News with its pernicious influence on American politics). These media support rightwing politicians and – in Australia at least – consistently downplay the importance of climate change, making effective action to limit its impact impossible or difficult.
Would the public so easily have been swayed by social media if they would not already have been ‘primed’ by the mainstream media, i.e., rightwing TV, radio and newspapers?
We are not dealing with some phenomenon that has at best some secondary importance, but one that is central to the functioning of democracy. The ‘West’ lauds itself for its ‘freedom’ and even went to wars to ‘defend’ it. But if a war is fought it should be against the pernicious spreading of lies and half-truths by the media, whether mainstream or social. If that war is lost, we may well be in big trouble very soon.
Die politische Entwicklung in Europa und der Welt: Februar – Mai 2016. Selbst wenn die Grossmächte einen Krieg um alles vermeiden wollen, Fehlkalkulationen sind immer möglich. Heidegger und die Politik. Russland, Saudiarabien, Israel, Iran, Syrien und Iraq
Im folgenden meine emails, die die politische Entwicklung in Europa und der Welt zwischen Anfang Februar bis Ende Mai 2016 kommentieren
30 Mai 2016
Der Prime Minister von Malaysia hat 600 (oder 900?) Millionen A$ auf
seinem Privatkonto aus Saudiarabien. Malaysia war bisher ein Land mit
tolerantem Islam. Die Situation wird laufend weniger tolerant. Ist das
wohl verbunden mit der Geldüberweisung?
23 Mai 2016
Stimmt das? Wenn ja, gefährliches Abkommen. Die Verantwortlichen sollten
³gesackt² werden.
https://www.rt.com/news/343893-turkey-europe-qualified-refugees/
Auszug:
“During the same meeting, representatives of Germany, the Netherlands
and Luxembourg reportedly told the assembly that over the past weeks
Turkish authorities have repeatedly been rejecting exit applications
filed by Syrian well-trained engineers, doctors and other professionals,
who could successfully integrate into European societies.
Under
the controversial migrant deal, Brussels has given Ankara exclusive
rights to select refugees permitted to leave the country and re-settle
into the EU. Previously, the UNHCR, which was in charge of this
procedure, has been ³officially informed² by Turkish authorities that
Syrian academics will ³no longer be allowed to travel to Turkey,² Spiegel
wrote.”
21 Mai 2016
Vielen Dank. Was klar wird ist, dass sowohl in Georgien und in der Krim
Russland auf Aktionen reagierte, die es als gegen sich gerichtet sah. Der
³Westen² gab Georgien und der Ukraine moralische, mediale und militärische
Unterstützung, ohne dass man versuchte, Russlands Position zu verstehen.
Merkels Politik läuft in die gleiche Richtung. Wo bleibt die deutsche
Presse? Warum werden diese entscheidend wichtigen Probleme (Möglichmeit
eines Atomkrieges usw.) nicht mit dem Nachdruck diskutiert, die sie
verdienen? Und wo bleibt die deutsche Intelligenz, insbesondere Akademia?
Man schlittert, wie es scheint unaufhaltsam, einer Katastrophe entgegen.
In meiner früheren email hatte ich vergessen, einen weiteren ³Höhepunkt²
zu erwähnen: Israel hat sich erneut geweigert, einem diesmal von
Frankreich initiierten Ländertreffen beizutreten, um Frieden mit den
Palästinensern zu machen. Und Israel hat jetzt auch sein Antiraketensystem
von U-Booten aus getestet. Also: nicht Verhandlungen und Kompromisse,
sonder Militär!
23 Mai 2016
Sicherlich ist Russland kein Unschuldshase. Aber es geht ja vor allem
darum, eine gefährliche Eskalation zu vermeiden, von der Deutschland
besonders betroffen wäre wegen seiner exponierten Lage und den Atomwaffen
nahe einem dicht besiedelten Gebiet. In anderen Worten, ein starker
Kanzler oder eine starke Kanzlerin sollte alles in seiner/ihrer Macht tun,
um zu vermeiden dass sich Russland provoziert fühlt.
21 Mai 2016
Und noch ein Punkt: Die USA halten es für fast selbstverständlich, dass
sie das Recht haben, in ihrer Nähe einzugreifen, wenn sie ihre Interessen
bedroht sieht, siehe die Kubakrisis und ihr Eingreifen in Granada. Die
Monroe-Doktrin! Und nicht nur in unmittelbarer Nähe, siehe die
Kolonisierung der Philippinen. Andere Staaten machen nur nach, was ihnen
vorgemacht worden ist.
19 Mai 2016
“Darauf verstaerke Russland seine
Truppen dort. Jetzt fand die NATO, dass diese Einheit nur fuer Kleinkrieg
stark genug ist. Regulaere russische Truppen wuerden sie ueberrollen,
bevor sie kampfbereit waere. Daher jetzt die 4 Bataillone oestliche der
Oder.” ——— Und zudem noch Raketenabwehr in Rumänien, angeblich um Europa
vor dem Iran zu schützen.
Und nicht zu vergessen, die sich zuspitzende Lage im Südchinesischen Meer,
und das grosse Fragezeichen Trump. Nicht unwahrscheinlich, dass er
amerikanischen Präsident wird. Will sich angeblich mit Putin und Kim
(Nordkorea) treffen, aber wie sieht er China?
18 Mai 2016
Das ist, wie Du weisst, in den letzten ein bis zwei Wochen passiert:
1.) Erdogan will die Immunität von 138 Parlamentsabgeordneten, vorwiegend
kurdischen, aufheben und damit praktisch eine Diktatur errichten.2.)
Saudiarabien finanziert 5 oder 6 Radiostationen in Indonesien, die laufend
Sendungen über die saudiarabische Version des Islam bringen; die Lage in
Indonesien, immerhin der grössten moslemischen Nation, die bisher einen
ausgesprochen toleranten Islam vertrat, wird deutlich weniger tolerant:
mehr Freiwillige, die sich dem IS anschliessen wollen, usw.3.) Die kaum
weit respektierte, aber von der ³internationalen Gemeinschaft² anerkannte
Regierung in Libyen soll mit westlichen Waffen versorgt werden.4.)Es ist
nicht unwahrscheinlich, dass Grossbritanien die EU verlassen wird,
zumindest macht Johnson dafür Propaganda, mit deutlich antideutscher
Rhetorik.5.) Die EU-Kommission hat Pläne vorgelegt, Atomkraftwerke in
Europa zu fördern und sich damit in direkten Gegensatz zur deutschen
Politik gesetzt: damit liefert sie Argumente für diejenigen, die es für
falsch halten, dass nicht gewählte Bürokraten die Politik bestimmen (ein
Grund, warum Grossbritanien die EU verlassen will). 6.)Und noch einmal die
Türkei, der Premierminister zurückgetreten und die Möglichkeit, dass er
ersetzt wird mit einem engen Verwandten Erdogans, vielleicht einem der an
dubiosen Ölgeschäften mit dem IS verwickelt ist.
Kaum Fortschritte in Syrien und Deutschland quasi verbündet mit den
Hauptschuldigen an der Situation dort, nämlich Saudiarabien und Türkei.
Ist es wirklich klug, 75 Millionen Türken visumfreie Einreise nach Europa
zu gewähren?
9 Mai 2016
Russland wird auf jeden Fall immer mit Massnahmen reagieren, die die des
Westens übertreffen, weil es logistisch am stärkeren Hebel sitzt. Die
Frage ist: wie lange kann das so weitergehen, bevor es zum Knallen kommt?
Und all das passiert, ohne dass die deutsche Presse (und die in anderen
europäischen Ländern) das Publikum auf die gefährliche Entwicklung mit
Nachdruck hinweist. Fussball und Eurovision sind anscheinend wichtiger.
5 Mai 2016
Danke. Wir driften (oder eilen?) einer gefährlichen Situation entgegen.
Jetzt brauchte man mehr denn je eine starke Führung in Deutschland, und
Europa. Stark im Sinn von klarem Kopf und Einsicht, was man machen sollte,
um nicht in eine völlig aussichtslose Lage zu geraten. Vor allem auch,
weil die politische Führung in den USA sich radikal ändern könnte.
3 Mai 2016
U-Boote: Deutschland hat ja schon einige Pannen erlebt: z.B. Die
wiederholte Verzögerung der Inbetriebnahme des Berlin-Brandenburgischen
Flughafens. Wie ich vor einiger Zeit schrieb: importiert einige 10000
chinesische Ingenieure und er wäre garantiert bald fertig. Was die U-Boote
anbetrifft, Turnbull, der australische Primaminister, hat sich auf ein
riskantes Spiel eingelassen. Das U-Boot gibt es noch garnicht, das
Propulsion-System gibt es noch nicht, viele der einzubauenden
Waffensysteme gibt es noch nicht. Die Sache ähnelt der Seewolf-Affäre in
den USA: ein U-Boot wurde geplant, das noch nicht einmal auf dem
Reissbrett bestand, um einer befürchteten russischen U-Boot Gefahr zu
begegnen. Die Sache verzögerte sich wiederholt, man produzierte
schliesslich drei der Boote und das Programm wurde abgeblasen. Viele
Milliarden Dollar down the rain. Einige der Berater, die die australische
Regierung jetzt über das U-Boot-Programm berieten, waren übrigens in die
Seewolf-Affaire verwickelt (nach der Financial Review, einer der seriösen
australischen Zeitungen).
Guiodo Westerwelle: Er war ja auch anscheinend weitgehend dafür
verantwortlich, dass sich Deutschland nicht in das Libyen-Debakel
einliess. Eine Alternative heute:????????? Angela Merkel doch wohl kaum,
vielleicht Steinmeier.
Konzessionen der Sowjetunion und der USA: Die erstere zog sich aus
Deutschland zurück, die letztere ist immer noch dort.
26 April 2016

Ein Photo von Merkel und Obama im heutigen Sydney Morning Herald (26.4.16).
Fast lächerlich. Die Musterschülerin wird von ihrem Lehrer gelobt. Merkel
die Statthalterin der USA in Europa. Lächerlich wenn¹s nicht so gefährlich
wäre.
24 April 2016
Und um es nicht zu vergessen, die von mir erwähnten Geschäfte drehen sich meist um den Verkauf von Kriegsgeräten. Und: Saudiarabien hat finanziert und finanziert das Atomprogramm in Pakistan.
24 April 2016
Wie ich gerade hörte (auf einer TV-Diskussion, an der auch ein
muslimischer Experte teilnahm), benutzt der IS die gleichen Lehrbücher für
religiöse Indroktinierung, die auch an renommierten saudiarabischen
Universitäten benutzt werden. Gosse Moscheen in verschiedenen europäischen
Ländern sind von Saudiarabien gebaut und mit Imamen versorgt worden.
Deutschland macht aber grosse Geschäfte mit dem Land.
James Baker, der amerikanische Aussenminister zur Zeit der
Wiedervereinigung, sprach im Bundestag aus Anlass des Gedenkens an
Genscher. Gorbachev war nicht dort. War er nicht eingeladen worden oder
wollte er nicht? In jedem Fall, wieder einmal eine vermisste Chance, das
Verhältniss zu Russland zu verbessern. In diesem Zusammenhang, Obama will
anscheinend bei seinem Deutschlandbesuch darauf drängen, das sich die
Bundesrepublik starker militärisch in den osteuropäischen Ländern
engagiert.
20 März 2016
All das, was in Polen während und nach dem Krieg passierte, stimmt so
ungefähr überein mit dem, was mir mein russischer Freund (der in Kiew
lebte und selbst Jude ist) über die Judenverfolgung in der Ukraine während
des Krieges erzählte (siehe eine meiner früheren emails).
Klaus
http://www.tabletmag.com/jewish-arts-and-culture/books/194312/anna-bikont-j
edwabne
14 März 2016
Ja, sicher, wir sind alle ‘Schweine’. Sollte man deswegen auf politische
Stellungnahmen verzichten? Wenn man die politischen Debatten in
Deutschland und Australien vergleicht, scheinen sie mir viel reifer und
vernünftiger in Deutschland zu sein. Hier in Australien geht es immer um
etwas mehr Steuern oder weniger, und deswegen werden Parteien gewählt.
Flüchtlinge: gelegentlich mal Proteste gegen die australische
Flüchtlingspolitik von Kirchen (aber nicht allen) und den Grünen, sonst
nichts. – Und was die USA angeht, unreifer geht es wohl kaum, und jeden
Tag etwa 90(?) Tote durch gun fire.
Die AfD sitzt jetzt solide in immerhin drei Landtagen, aber es hätte ja
schlimmer ausgehen können, und nicht alle in der Partei scheinen mir
rechtsextrem zu sein.
13 März 2016
Die Kommentare über Merkels Flüchtlingspolitik sind sehr interessant.
Unter anderem:
‘Es wird immer deutlicher, die Kaiserin ist nackt. Merkel hat Deutschland
völlig isoliert und ist selbst jetzt nicht bereit, die Realität
anzuerkennen. Die Probleme der arabischen Welt können nicht mit
Masseneinwanderung gelöst werden. Der Rücktritt Merkels ist überfällig,
denn nur so kann ein Neustart der Flüchtlingspolitik gelingen.¹
‘Gut so!
<http://meta.tagesschau.de/id/109438/widerstand-in-der-eu-gegen-tuerkei-dea
l-waechst#comment-2462120>
Hoffentlich können die anderen Länder Merkels
Flüchtlingswahnsinn noch stoppen. Bei uns scheint ja niemand mehr in der
Lage zu sein ihren Alleingang zu beenden. Ich hoffe wirklich inständig
das dieses Desaster sie am Ende doch noch das Amt kostet.’
8 März 2016
Wie man liest, will Erdogan jetzt bedeutend mehr von der EU, ???
Milliarden, Zugeständnisse beim Visazwang, Beschleunigung der
Verhandlungen zum Europabeitritt der Türkei, usw. Ich nehme an, dass man
Massnahmen trifft, dass die Gelder nicht ohne Umwege direkt in Erdogans
Tasche fliessen. Immerhin steht sein Sohn im Verdacht (in Italien u.a.),
in Geldwäsche verwickelt zu sein. Die grösste regierungskritische Zeitung
ist gerade gleichgeschaltet worden. Erdogan braucht also keine
Enthüllungen zu befürchten. (Najib in Malaysia strich ja nur etwa eine
Milliarde Aus $ ein (oder sind es inzwischen mehr ?)).
Die EU hat sich mit ihrer Politik in eine Situation gebracht, in der man
Erdogan praktisch alles liefert was er will, ohne wirksame Garantien für
eine Reduzierung der Flüchtlingszahlen zu bekommen. Sie hat ihm praktisch
auch freie Hand für die Unterdrückung der Kurden (auch in Syrien) gegeben,
wodurch die Friedensverhandlungen für Syrien gefährdet werden.. —
Alternativen: sperrt die türkische Grenze und setzt Erdogan unter Druck. –
Und Kooperation mit Russland. Nur so kann man, wie mir scheint, eine
schnelle Lösung des Syrienkonfliktes erreichen.
6 März 2016
https://www.rt.com/op-edge/334378-us-defense-establishment-putin/
Auszug:
However, Farkas¹s perspective outlines all that¹s wrong with how the
US interacts with the rest of the world today. She¹s calling for the
defeat of a leader with 80 percent approval ratings, because he doesn¹t
support US foreign policy objectives. If Putin prevents America taking
over the world, he must be removed. It¹s Doctor Evil stuff.
This
fanatical analyst believes that Russia is a threat to America. However,
it¹s NATO which has been expanding during the past two decades, while
Moscow has taken a defensive, often highly reactionary posture. For
example, in Syria, Assad¹s forces had the upper hand in Aleppo and would
surely have taken the city, but Putin agreed a ceasefire rather than
continue the bloodshed there. A real-life expansionist warmonger would
have kept the fighting going.
In reality, it¹s America which has
been aggressive in this century. Illegally invading Iraq, destroying
Libya, facilitating the collapse of Yemen and the Syrian Civil War. In
Russia¹s backyard, Washington has openly fomented uprisings in Georgia
and Ukraine, the results of which have subsequently been rejected at the
ballot box. The US-backed regimes in Kiev and Tbilisi were both
eventually voted out after the ³Orange² and ³Rose² revolutions. The
current ŒMaidan¹ administration in Kiev now has lower approval ratings
<https://www.rt.com/news/327254-ukraine-approval-radings-drop/> than the
democratically elected, if corrupt, government it replaced.
Read more
Friend or foe? State Dept, Pentagon split on whether
Russia poses threat
<https://www.rt.com/usa/333675-russia-pentagon-enemy-kerry/>
This indicates that they were never popular upheavals to begin
with, but rather driven by capital city liberals, without mass backing
in the provinces.
28 Februar 2016
Ich habe mehrfach versucht, mich durch die Prosa Heideggers zu lesen, aber
immer ohne Erfolg. Daher hat mich immer überrascht, dass er der
einflussreichste (oder einer der einflussreichsten) modernen Philosophen
ist, insbesondere auch wegen seiner Nazisympathien. Der Aufsatz unten
zeigt mir, dass er enormen politischen Einfluss ausgeübt hat und ausübt,
unter anderem auch im Iran und Russland. Manches an Putins Politikword mir
jetzt besser verständlich. Russland unter Putin und schon immer in der
Vergangenheit respektiert die Kultur der Minderheiten, der Westen (USA,
Australien, Canada) hat immer versucht, sie kulturell zu absorbieren und
auszulöschen, um nur ein Beispiel zu nennen.
http://www.the-american-interest.com/2016/02/25/heideggers-ghosts/
“What, then, does Heidegger bequeath to his successor opponents of a
universalist, purportedly rationalist political order such as the
post-Cold War, liberal West?In the first place, Heidegger offers a
diagnosis of such an order that punctures its claims to benign
universalism. The diagnosis holds that the widespread sense of
alienation that characterizes ³modern² or ³bourgeois² life derives from
an excessive and unwarranted emphasis on reason as a way of
ordering and justifying our existence, and that this has resulted,
further, in an orientation to others and the world that is excessively
aggressive and violent. Heidegger understands ³reason² not as a
timeless, universal means by which humanity can rise above itself, but
as a defective instrumentality born in violence at a specific moment in
history. That instrument subsequently spread in such a fashion that it
now expresses itself principally through technological forms of
domination. It masks itself, but it is inherently hegemonic and
dominating, distorting and excluding other modes of relating to the
world and other ways individuals can relate to one another. Heidegger¹s
diagnosis is broadly felt and very influential, having been taken up by
his Iranian and Russian followers‹as Gharbzadegi in Iran and as the
bankrupt ³three political theories² by Dugin‹as well as by his legatees in
the academy.”
22 Februar 2016
Danke für die Hinweise.Ich habe die Artikel nicht gelesen aber die
Situation ist ja klar. Selbst wenn die Grossmächte einen Krieg um alles
vermeiden wollen, Fehlkalkulationen sind immer möglich, und ich glaube
zwei Staaten zu kennen, die an einem Krieg durchaus interessiert ein
könnten, und das sind die Türkei und Saudiarabien. Die Türkei, weil sie
von Anfang an darauf gesetzt hat, Assad zu stürzen, und jetzt in der Falle
sitzt. Solange es einen funktionierenden syrischen Staat gab, war Syrien
vor den syrischen Kurden so einigermassen sicher, jetzt ist sie es nicht
mehr. Saudiarabien, weil es sein korruptes Regime durch den weit
liberaleren Shiismus bedroht sieht. Und wie üblich, steht Deutschland auf
der falschen Seite. – Aber es gibt einen Hoffnungsschimmer, wie man hört,
wollen Obama und Putin die Situation besprechen und entschärfen. Wenn die
USA und Russland ihre gleichliegenden Interessen im Kampf gegen den Terror
im Nahen Osten, d.h. einen funktionierenden syrischen Staat zu etablieren,
zur Grundlage ihrer Politik machten, könnte die Krise bald vorüber sein.
Merkel stösst Putin vor den Kopf wenn immer möglich, und Gauck macht da
kräftig mit. Die beiden scheinen mir das Stärkeverhältnis in der Welt
misszuverstehen.
Cameron: wie es scheint, will GB das sinkende Schiff verlassen.
14 Februar 2016
In der türkischen Region Aleppo bombardiert die Türkei kurdische Milizen
(nicht etwa die IS), und sie erwägt auch, gemeinsam mit Saudiarabien, den
Einsatz von Bodentruppen in Syrien (Spiegel online heute). Russland ist in
Syrien auf Einladung der legitimen syrischen Regierung (des Assad-Regimes
in westlicher Terminologie), Saudiarabien und die Türkei sind Aggressoren.
Wenn man sich also die heutige Konstellation ansieht: Deutschland
quasi-alliiert mit der Türkei und Saudiarabien, das letztere wohl das
rückständigste und autoritärste Regime im Nahen Osten. Die Türkei
mitverantwortlich für die Erfolge des IS (fast alle nichtsyrischen Kämpfer
des IS durch die Türkei eingeschleust, medizinische Betreuung von
IS-Kämpfern in der Türkei, Verfolgung von Akademikern und Journalisten,
die über die Unterstützung der Türkei für den IS berichten, Unterdrückung
der kurdischen Terrormilizen (in türkischer Terminologie), usw. — Russland
alliiert mit Syrien und dem Iran. Damaskus heute eine Stadt, in der
Aleviten, Sunnis, Shiiten und Christen usw. zusammenleben. Im Iran ein
weit liberalerer Islam als in den meisten anderen Ländern der Gegend. –
Wie mir scheint, liegt das primäre Interesse der Türkei darin, die Kurden
unten zu halten, die USA schienen von Anfang an vor allem darauf bedacht,
Russland unten zu halten. – So sehen es die Russen: Russland ist vom
Westen (sprich USA) im Stich gelassen worden, wie es auch gerade wieder in
München auf der Sicherheitskonferenz klar wurde.
Deutschland!?: völlig verfehlte Politik. Auch Frankreich hat ja gerade
erklärt, keine Flüchtlinge mehr aufzunehmen.
The European crisis. Die Europakrise 2016.
Das letzte halbe Jahr hat Entwicklungen gesehen, die unsere politische Zukunft entscheidend beeinflussen werden: der Brexit und Stärkung der politischen Rechten in Europa, die Wahlen in den USA, die die Konservativen entscheidend gestärkt haben, und militärische Entwicklungen im Nahen Osten und Südostasien. Dieser Post verfolgt diese Entwicklungen anhand meiner emails seit Juni 2016. -The last half year has seen developments that may have enormous consequences for our political future: the brexit and strengthening of the political Right in Europe, the elections in the US which have decisively strenghtened the conservatives, and military developments in the Near East and Southeast Asia. This post documents these developments using my emails since June 2016.
Siehe auch hier, see also here: http://krohde.wordpress.com
28 November 2016
Jetzt tritt also in Frankreich ein anscheinend prorussischer Mann als
Präsidenten-Kandidat der Konservativen an, und eine prorussische Dame als
Kandidatin der Ultrarechten. In den USA hat ein Mann gewonnen,der es ganz
klar gemacht hat, dass er bessere Beziehungen zu Russland will – In
Estland ist vor kurzem die sehr prowestliche Regierung gestürzt (ich habe
nicht verfolgt,wie sich die Lage weiter entwickelt). Wenn Deutschland
nicht sehr aufpasst, manövriert es sich in eine ausweglose Ecke.
6 Oktober 2016
http://www.commondreams.org/views/2016/10/05/dangerous-new-group-think-war-
syriarussia
“Not since the eve of the U.S. invasion of Iraq has Official
Washington’s political/punditry class clamored more single-mindedly –
and openly – for the U.S. government to commit a gross violation of
international law, now urging a major military assault on the government
of Syria while also escalating tensions with nuclear-armed Russia.
And, like the frenzied war fever of 2002-2003, today’s lawless
consensus is operating on a mix of selective, dubious and false
information – while excluding from the public debate voices that might
dare challenge the prevailing “group think.” It’s as if nothing was
learned from the previous disaster in Iraq.
“Like the frenzied war fever of 2002-2003, today’s
lawless consensus is operating on a mix of selective, dubious and false
information.”
Most notably, there are two key facts about Syria that Americans are
not being told: one, U.S. regional “allies” have been funding and arming
radical jihadist groups, including Al Qaeda terrorists, there almost
since the conflict began in 2011
https://consortiumnews.com/2015/07/20/hidden-origins-of-syrias-civil-war/
and, two, the claim about “moderate” Syrian rebels is a fraud
https://consortiumnews.com/2016/09/29/how-the-us-armed-up-syrian-jihadists
/;
the “moderates” have served essentially as a P.R. cut-out for the U.S.
and its “allies” to supply Al Qaeda and its allies with sophisticated
weapons while pretending not to.
For Americans who may find those two points hard to believe, they should
remember that the United States and Saudi Arabia went in 50/50 with
billions of dollars
https://consortiumnews.com/2013/04/07/hollywoods-dangerous-afghan-illusion
/
to finance the jihadist mujahedeen in Afghanistan in the 1980s, viewing
these religious fanatics as a useful “tip of the spear” to kill Soviet
troops who were defending the leftist secular regime then governing in
Kabul.
That exercise in U.S.-Saudi realpolitik gave birth to the modern
jihadist movement, bringing together a network of foreign jihadists, led
by Saudi Arabia’s Osama bin Laden (which morphed into Al Qaeda), with
Afghan/Pakistani extremists who evolved into the Taliban.
Though U.S. officials eventually came to fear this Frankenstein
monster that they had helped create, Saudi intelligence continued to
work with Al Qaeda and its affiliates, using them as a kind of
international paramilitary force to punish Saudi enemies, particularly
Shiite-dominated governments, from Iran to Syria to now Iraq.
The Saudis also began collaborating with Israel
https://consortiumnews.com/2015/04/15/did-money-seal-israeli-saudi-allianc
e/,
which shared Riyadh’s view that Iran and the “Shiite crescent”
represented a strategic threat. Between Saudi money and Israeli
political clout, the two countries could fend off occasional fits of
U.S. anger, even to the point of getting the U.S. government to hide a
29-page chapter about Saudi financing for the 9/11 hijackers
https://consortiumnews.com/2016/07/16/the-long-hidden-saudi-911-trail/
from the congressional 9/11 report for a dozen years.”
ETC.ETC.
2 Oktober 2016
Volkswagen, Deutsche Bank, Commerzbank, Ausverkauf deutscher
Hightech-Firmen an China, usw.usw. (vor Jahren der Verkauf von Mannesmann).
Wer leidet, wer streicht die Gewinne ein? Und gibt es rechtliche
Möglichkeiten, Geschäfte zu unterbinden, die von ³Managern² vorwiegend zum
eigenen Nutzen gemacht werden?
http://www.spiegel.de/wirtschaft/unternehmen/deutsche-bank-wem-nuetzt-das-g
roesste-geldhaus-des-landes-a-1114734.html
“24,4 Milliarden Euro hat die Deutsche Bank allein von 2009 bis 2015
ihren (vor allem leitenden) Mitarbeitern an Boni gezahlt. Für die
exzessiven Jahre 2006 bis 2008, als einzelne Banker 80 Millionen Euro
Bonus erhielten, nennt die Bank auf Anfrage keine Zahlen. An Dividenden
jedenfalls hat die Bank im gesamten Zeitraum von 2006 bis 2015 knapp 5,2
Milliarden Euro an ihre Aktionäre ausgeschüttet.”
24 September 2016
“Die Franzosen freuen sich darueber (z.B.
Rafale Duesenjaeger an Indien) und die Deutschen schaemen sich darueber
(Panzer an Araber).²
Hier fehlt etwas: füge am Ende hinzu: ³und die Deutschen zahlen die Zeche
(Flüchtlingsflut, Truppen in Mali usw., um die Kolonialpolitik anderer
fortzuführen²).
Übrigens: Deutschland hat wenige Trümpfe, und einer der letzten (Hightech
Firma, die wesentlich würden deutschen Maschinenbau ist) ist gerade an
China verkauft worden. Welche Garantieren hat man eigentlich dafür, dass
dies nicht in nicht zu ferner Zukunft zum Kollaps des deutschen
Maschinenbaus, wesentlich für die deutsche Exportindustrie, führen wird?
22 September 2016
Aus dem Guardian online:
“One of the recurring themes of Donald Trump’s national security
strategy is his plan to “take the oil” in Iraq and from areas controlled
by Islamic State <https://www.theguardian.com/world/isis>
(Isis) extremists. It would drain Isis’s coffers and reimburse the US
for the costs of its military commitments in the Middle East, the
candidate insists.
At a forum hosted by NBC on 7 September, Trump suggested oil seizure would have
been a way to pay for the Iraq war, saying: “We go in, we spend $3tn, we
lose thousands and thousands of lives, and then … what happens is we
get nothing. You know, it used to be to the victor belong the spoils.”
He added: “One of the benefits we would have had if we took the oil
is Isis would not have been able to take oil and use that oil to fuel
themselves.”
22 September 2016
http://www.commondreams.org/news/2016/09/21/indifferent-yemens-misery-senat
e-approves-massive-saudi-arms-deal
“The U.S. Senate on Wednesday voted overwhelmingly to dismiss a bipartisan
bill that would have blocked
http://www.commondreams.org/news/2016/09/08/civilian-deaths-rising-efforts
-block-us-saudi-arms-sale-gain-steam
a massive $1.15 billion weapons shipment to Saudi Arabia, to the dismay
of peace groups and rights advocates who have called on the U.S. to end
its support for the brutal Saudi bombing campaign in Yemen.
The bipartisan resolution to block the weapons sale failed 71-27
http://www.senate.gov/legislative/LIS/roll_call_lists/roll_call_vote_cfm.c
fm?congress=114&session=2&vote=00145, with two senators not voting.
During the floor debate, many of those in favor of the weapons sale
echoed Sen. Bob Corker (R-Tenn.), who declared: “This is a sale that
benefits us.” Although even Corker admitted Saudi Arabia is not a
“perfect ally” and that many civilians had been killed in Yemen, he
argued that the massive sale of new weapons should be approved because
it will benefit the U.S. economically. Corker further claimed that
arming the Saudi regime serves U.S. geopolitical interests by pushing
back against the Iranians, who support the anti-Saudi Houthi factions in
Yemen.”
f.).
20 September 2016
http://www.commondreams.org/news/2016/09/19/supplying-white-phosphorus-saud
is-new-claims-reinforce-us-war-crimes-complicity
This seems to correspond to what happened in the Iraq-Iran war, when
Saddam Hussein was still the favourite dictator of the U.S.
20 September 2016
Dies ist die eigentliche Schuld Angela Merkels, dass sie sich praktisch
kritiklos als Vollzugsorgan amerikanischer Politik sieht. Siehe Ukraine
und Syrienflüchtlinge.
Ein Artikel von John Parry (Robert Parry broke many of the Iran-Contra
stories in the 1980s for the Associated Press and Newsweek. His latest
book, Neck Deep: The Disastrous Presidency of George W. Bush
<http://www.amazon.com/dp/1893517039?tag=commondreams-20/ref=nosim>, was
written with two of his sons, Sam and Nat. His two previous books are
Secrecy & Privilege: The Rise of the Bush Dynasty from Watergate to Iraq
http://www.amazon.com/dp/1893517012?tag=commondreams-20/ref=nosim and
Lost History: Contras, Cocaine, the Press & ‘Project Truth’
http://www.amazon.com/dp/1893517004?tag=commondreams-20/ref=nosim.)
http://www.commondreams.org/views/2016/09/19/americas-worldwide-impunity
Auszüge:
“After several years of arming and supporting Syrian rebel groups that
often collaborated
https://consortiumnews.com/2016/02/16/obamas-moderate-syrian-deception/
with Al Qaeda’s Nusra terror affiliate, the United States launched an
illegal invasion of Syria two years ago with airstrikes supposedly aimed
at Al Qaeda’s Islamic State spin-off, but on Saturday that air war
killed scores of Syrian soldiers and aided an Islamic State victory.
Yet, the major American news outlets treat this extraordinary set of
circumstances as barely newsworthy, operating with an imperial hubris
that holds any U.S. invasion or subversion of another country as simply,
ho-hum, the way things are supposed to work.
In the world of Official Washington, the United
States has the right to intervene anywhere, anytime, for whatever reason
it chooses.
On Monday, The Washington Post dismissed the devastating airstrike at
Deir al-Zour killing at least 62 Syrian soldiers as one of several
“mishaps” that had occurred over the past week and jeopardized a limited
ceasefire, arranged between Russia and the Obama administration.
But the fact that the U.S. and several allies have been routinely
violating Syrian sovereign airspace to carry out attacks was not even an
issue, nor is it a scandal that the U.S. military and CIA have been
arming and training Syrian rebels. In the world of Official Washington,
the United States has the right to intervene anywhere, anytime, for
whatever reason it chooses.
President Barack Obama even has publicly talked about authorizing
military strikes in seven different countries, including Syria, and yet
he is deemed “weak” for not invading more countries, at least more
decisively.
Democratic presidential nominee Hillary Clinton has vowed to engage
in a larger invasion of Syria, albeit wrapping the aggression in pretty
words like “safe zone” and “no-fly zone,” but it would mean bombing and
killing more Syrian soldiers.
As Secretary of State, Clinton used similar language to justify
invading Libya and implementing a “regime change” that killed the
nation’s leader, Muammar Gaddafi, and unleashed five years of violent
political chaos.
If you were living a truly democratic country with a truly
professional news media, you would think that this evolution of the
United States into a rogue superpower violating pretty much every
international law and treaty of the post-World War II era would be a
regular topic of debate and criticism.
Those crimes include horrendous acts against people, such as torture
and other violations of the Geneva Conventions, as well as acts of
aggression, which the Nuremberg Tribunals deemed “the supreme
international crime differing only from other war crimes in that it
contains within itself the accumulated evil of the whole.”
……………
“On Sunday, the Times also asserted as flat fact the dubious charge
against Assad that he has “hit civilians with gas attacks” when the most
notorious case – the sarin attack outside Damascus on Aug. 21, 2013 –
appears now to have been carried out by rebels
https://consortiumnews.com/2014/04/07/the-collapsing-syria-sarin-case/
trying to trick the United States into intervening more directly on their
side.
A recent United Nations report blaming Syrian forces for two later attacks
involving chlorine was based on slim evidence
https://consortiumnews.com/2016/09/08/un-team-heard-claims-of-staged-chemi
cal-attacks/
and produced under great political pressure to reach that conclusion –
while ignoring the absence of any logical reason for the Syrian forces
to have used such an ineffective weapon and brushing aside testimony
about rebels staging other gas attacks.”On Sunday, the Times also asserted
as flat fact the dubious charge
against Assad that he has “hit civilians with gas attacks” when the most
notorious case – the sarin attack outside Damascus on Aug. 21, 2013 –
appears now to have been carried out by rebels
https://consortiumnews.com/2014/04/07/the-collapsing-syria-sarin-case/
trying to trick the United States into intervening more directly on their
side.
A recent United Nations report blaming Syrian forces for two later attacks
involving chlorine was based on slim evidence
https://consortiumnews.com/2016/09/08/un-team-heard-claims-of-staged-chemi
cal-attacks/
and produced under great political pressure to reach that conclusion –
while ignoring the absence of any logical reason for the Syrian forces
to have used such an ineffective weapon and brushing aside testimony
about rebels staging other gas attacks.”
18 September 2016
https://www.theguardian.com/us-news/2016/sep/14/corporate-cash-john-doe-fil
es-scott-walker-wisconsin
‘The pervasive influence of corporate cash in the democratic process,
and the extraordinary lengths to which politicians, lobbyists and even
judges go to solicit money, are laid bare in sealed court documents
leaked to the Guardian.
The John Doe files amount to 1,500 pages of largely unseen material
gathered in evidence by prosecutors investigating alleged irregularities
in political fundraising. Last year the Wisconsin
https://www.theguardian.com/world/wisconsin
supreme court ordered that all the documents should be destroyed,
though a set survived that has now been obtained by the news
organisation.
The files open a window on a world that is very rarely glimpsed by
the public, in which millions of dollars are secretly donated by major
corporations and super-wealthy individuals to third-party groups in an
attempt to sway elections. They speak to a visceral theme of the 2016
presidential cycle: the distortion of American democracy by big business
that has been slammed by both Donald Trump and Bernie Sanders.
9 September 2016
Du hast Australien vergessen. In Tasmanian lag die Ermordetenrate bei fast
100%, im gesamten Australien weiss niemand. So ähnlich dürfte das auch in
den USA liegen. Lateinamerika? Die vom sogenanten Westen in Vietnam und im
Nahen Osten initiierten Morde sind schwer abzuschätzen, gehen aber
sicherlich in die Millionen. Der Mensch ist ein Raubtier.
Was die Zahlenvergleiche insgesamt anbetrifft, bin ich sehr skeptisch. Die
Angaben des jeweiligen Autors scheinen mir immer ihre persönlichen
Vorurteile widerzuspiegeln, ob Historiker oder nicht.
Hitler vs. Stalin: wie viele Leute auf der jeweiligen Seite waren
persönlich am Morden beteiligt, und wie viele wussten davon? Hitler
brüstete sich zumindest nicht mit dem was passierte, bei Stalin war es
aber Instrument der Politik. Das sah man in Brandenburg: was in den
Gefängnissen mit politischen Gefangenen (Honneker, Busch usw.) und in der
Heilanstalt mit Geisteskranken passierte, war streng geheim, die GPU mit
ihren grünen Mützen nach dem Krieg waren überall präsent!
7 September 2016
Ih habe mich immer gewundert, woher Du sie Zahlen hattest, die belegt
sollten, dass die Nazis viel schlimmer als die Soviets gewesen waren,
zumindest was die Zahl der Ermordeten anbetrifft. Das Buch unten (und noch
mehr der Reviewer) sehen das allerdings anders. Und: ist die These des
kürzlich verstorbenen Historikers Nolte, dass der Nazimus eine Reaktion
auf den Bolschewismus war, wirklich so abwegig?
30 August 2016
http://www.tagesspiegel.de/politik/saudi-arabiens-neuer-botschafter-im-inte
rview-wir-wollen-einen-moderaten-und-toleranten-islam/13662394.html
Auszug:
Es gibt Anschuldigungen, dass Saudi-Arabien in Deutschland Moscheen baut
und Imame in unser Land entsendet. Ist das der Fall?
Definitiv
nicht. In Deutschland kann keine Moschee ohne die Erlaubnis Ihrer
Regierung gebaut werden. Und ich kann Ihnen mit hundertprozentiger
Sicherheit sagen, dass es keinen Antrag meines Landes diesbezüglich
gibt. Das Gleiche gilt für die angebliche Entsendung von Imamen. Diese
Anschuldigungen sind frei erfunden und basieren nicht auf Tatsachen.
30 August 2016
Today¹s Sydney Morning Herald: Peter Hatcher: We help to pay of terorism
at the petrol pump.
Extracts.
‘The barbaric punishments that Daesh hands out? It’s no coincidence
that they’re identical to the religious penalties or hudud that the
Saudi government inflicts on its people death for homosexual acts,
death by stoning for adultery or attempting to leave Islam, amputation
of a hand for stealing, and so on.
A former imam of Saudi Arabia’s
Grand Mosque in Mecca, Sheikh Adil al-Kalbani, said in January the
leaders of Daesh “draw their ideas from what is written in our own
books, our own principles”, according to The New York Times.
The
Saudi government and Saudi religious charities and Saudi
philanthropists have spent a fortune quietly funding Wahhabist mosques,
preachers and schools across the world in countries now struggling to
contain the threat of Daesh terrorism, countries from Belgium to
Indonesia.
How much have they spent on this global missionary
effort? A well-regarded professor of strategic studies at the Centre for
Policy Research in New Delhi, Brahma Chellaney, says: “Since the
oil-price boom of the 1970s, Saudi Arabia has spent more than $US200
billion on its global jihad project, including funding Wahhabi
madrassas, mosques, clerics and books.”
All of that has been
funded, ultimately, by the export of Saudi oil. By buying Saudi oil, we
in the West have funded the fomenting of the fundamentalist movement
that now assaults our security and our civilisation.
“Western
powers actually encouraged the kingdom as an antidote to communism and
the 1979 anti-US Iranian revolution to export Wahhabism,” Chellaney
says.
And even when there was not active encouragement from the
West, there has been the unending flow of great treasure to the kingdom.
The average cost of producing a barrel of oil in Saudi Arabia is about
$US9, the lowest in the world.
So whenever the world oil price is
above $US9 a barrel, the Saudis are making a profit. It has never been
anywhere near as low as $US9 in the entire post-oil shock era that began
in the 1970s. The lowest recent price was when it briefly hit $US15 in
2001.
The world price is currently in the high $US40s. In other
words, the West and others have kept the Saudis richly funded and well
bankrolled. And that has meant that Wahhabism has been well bankrolled,
too.
The West’s complicity in supporting its own most virulent enemies may not
be household knowledge, but it’s certainly no secret.
US
Vice-President Joe Biden made the point in a speech two years ago that
the Saudis and other “allies’ policies wound up helping to arm and build
allies of al-Qaeda and eventually the terrorist Islamic State”.
Washington has supported the House of Saud, with a military base in the
country, since 1945 under Roosevelt.
As the American resource academic Michael Klare explains in his book
Resource Wars:
“At the core of this arrangement is a vital but unspoken quid pro quo:
in return for protecting the royal family against its enemies, American
companies will be allowed unrivalled access to Saudi oilfields.”
And
the Saudi royal family has a power-sharing arrangement with the
country’s Wahhabist clerics. The government supports Wahhabism as the
state religion, and the clerics in turn endorse the legitimacy of the
Sauds as an absolute monarchy.
Counting only the countries where
Islam is a minority religion, Saudi Arabia has paid for the construction
of 1359 mosques, 210 Islamic centres, 202 colleges and 2000 schools, The
New York Times reported on the weekend.‹‹‹‹‹‹‹‹‹‹‹‹
‹‹‹‹‹‹‹
“We feel that we are under attack from the growing influence of
Wahhabists in Indonesia” preaching an alien literalist Islam, Monash
University law professor and Indonesian national Nadirsyah Hosen tells
me.
Considering the cost of Saudi-sponsored extremism to our
security, to our social cohesion, to civilised values everywhere, even
the cheapest oil price means that we pay for our petrol at an
incalculably high price.
21 August 2016
Die Entkommensroute für den IS mag so sein wie Du schreibst, die
allgemeine Einstellung der Amerikaner und ihrer Satelliten gegenüber Assad
und den verschiedenen Militias ist allerdings wohl so, wie in dem Artikel
beschrieben. Eine der islamischen Militias hat jetzt ihren Namen von Al
Quaida-gelinkt (El Nusra Front oder so ähnlich, glaube ich), geändert,
anscheinend
um für amerikanische Unterstützung zu qualifizieren. Lachhaft! – Und der
Yemen: unglaubliche Schweinerei der Saudis und Satelliten. In der
westlichen Presse jedoch weit weniger eingehend berichtet wie die
Ereignisse in Syrien. Es handelt ich ja immerhin um einen Verbündeten des
ŒWestens¹.
Dies dürfte Dich interessieren.Unser Sohn ist jetzt in Shanghai auf
Einladung der Chinesen. Hier ist was er schrieb:
³ŠŠ.. Not sure if you got my last email. I’m in Shanghai now.
Already spent the day at the institute. They don’t understand the
concept of Sunday’s here. They took me on a lab tour this morning. It
was quite mind-blowing how well-resourced the Chinese are. The West
will be the laughing stock of the Chinese if we don’t start catching
up. The government investment into the setup I saw this morning is
astronomical. I saw the prototype of the satellite they launched last
week. That launch alone was worth $100m. And the labs I saw today must
have been worth as much too. Peter.²
Immerhin, es gibt ja Aussichten (oder nicht?), dass der Berlin-Brandenburg
Flughafen eines Tages vielleicht doch fertig wird. Deutsche
Ingenieurskunst in ihrer vollen Stärke.
20 August 2016
Interesting and disturbing, if true.
http://www.globalresearch.ca/proof-us-and-nato-backed-rebels-are-not-fighti
ng-isis/5541559
3 August 2016
In diesem Zusammenhang, dies ging vor kurzem durch die australische Presse:
http://www.smh.com.au/world/australia-complicit-in-1965-anticommunist-purge
-in-indonesia-civil-tribunal-20160720-gqa0sh.html
‘The tribunal said the brutal murder of around 500,000 people was
aimed at annihilating a section of the population and could be
categorised as genocide.
ŠŠ…
A panel of seven international judges found Australia, Britain and
the US were all complicit to differing degrees in the commission of
these crimes.’
https://redflag.org.au/article/australias-role-1965-66-communist-massacres-
indonesia
2 August 2016
Mossadegh wollte die iranische Erdölindustrie verstaatlichen. Warum sollte
das nicht auch im Interesse des Schahs gewesen sein? Sicherlich war es
nicht im Interesse der westlichen, vor allem der britischen Erdölkonzerne.
Mossadegh lässt sich wohl kaum als kommunistischer Mitläufer einstufen.
Ulbricht: ein typischer kommunistischer Apparatschik. Glaubst Du im Ernst,
dass er gegen Stalins und seiner Nachfolger Wünsche gehandelt hätte,
zumindest in wesentlichen Punkten. Immerhin konnte die Sowjetunion im
Zweifelsfall ihre Wünsche mittels ihres Militärs in der Ostzone
durchsetzen. Bei Kim Il-Sung ist das wahrscheinlich anders.
23 Juli 2016
Jetzt haben wir die Bescherung, zuerst Würzburg, und jetzt München (falls
es sich tatsächlich um einen islamistisch motivierten Angriff handelt). Im
Osten Libyens soll Frankreich (ohne die von der UN anerkannte Regierung in
Tripolis unterrichtet zu haben) in Militäraktionen verstrickt sein;
Fortsetzung der alten Kolonialpolitik. Amerika soll verlangt haben, dass
sich alle westlichen Länder im Kampf gegen den IS stärker engagieren, und
zwar militärisch. Es sollte doch inzwischen klar sein, dass IS als eine
Folge des militärischen Engagements Amerikas und seiner Verbündeten im
Nahen Osten erst entstanden ist. Was Libyen anbetrifft, es sollte doch
inzwischen klargeworden sein, dass die Entfernung Gaddafis die Ursache der
Katastrophe ist, Frankreich auch hier die grössten Scharfmacher (wenn ich
mich recht erinnere, griffen sie als erste militärisch in Libyen gegen
Gaddafi ein). Und die Franzosen fragen sich entsetzt, nach dem Anschlag in
Nizza: warum tut man uns da an?
10 Juli 2016
Referendum in Estland? Mir scheint, dass man im Zweifelsfall annehmen
sollte, dass sich eine Minderheit wahrscheinlich für ihr ŒVaterland¹
entscheiden würde. Siehe Saarland usw.
2 Juli 2016
Piketty gibt Deutschland die Hauptschuld am Brexit, sieht aber
Möglichkeiten, wenn sich Merkel den Linksparteien nähere.
http://www.focus.de/politik/deutschland/kontinent-in-der-krise-star-oekonom
-piketty-gibt-deutschland-schuld-am-brexit_id_5690183.html
30 Juni 2016
Putin in der deutschen Schule in Moskau, in der auch seine Tochter ihren
Abschluss machten!
http://www.spiegel.de/schulspiegel/leben/wladimir-putin-besucht-deutsche-sc
hule-in-moskau-a-1100466.html
18 Juni 2016
http://www.spiegel.de/politik/ausland/frank-walter-steinmeier-kritisiert-na
to-manoever-in-osteuropa-a-1098360.html
Steinmeier scheint mir derzeit der vernünftigste deutsche Politiker in der
Regierung zu sein, indem er die Nato Manöver an der Grenze zu Russland
scharf kritisiert.
9 Juni 2016
Vielen Dank. Ich bin gerade in Adelaide, wo ich Œjudge¹ für den Waterhouse
Natural Science Arts Prize bin. Das judging ist getan, heute Abend st die
Eröffnung einer Ausstellung ausgewählter Werke durch den Minister für
Kunst der südaustralischen Regierung.
Flüchtlinge: eine der schlimmen Folgen der Masseneinwanderung in Europa
ist die ŒBekehrung¹ vieler Leute zur australischen Flüchtlingspolitik. Der
dramatische Rechsruck in Österreich ist eine voraussehbare Folge der
gleichen Erscheinung. Letzten Endes wird nichts anderes übrigbleiben, als
die Grenzen dicht zu machen, aber auf eine humane Art. – Die
Zusammenarbeit mit Erdogan, verständlich aber höchst problematisch. Die
türkische Politik ist ja mitverantwortlich zu machen für die katastrophale
Situation. Ebenso Bush: Afghanistan und Irak, Frankreich, die USA usw.:
Zusammenbruch in Libyen und in Nord- und Westafrika insgesamt.
2 Juni 2016
Nun hat sich auch der Dalai Lama zur Flüchtlingskrise in Europa und
Deutschland geäussert: Europa solle nicht muslimisch werden, gewährt den
Flüchtlingen zeitweiliges Asyl. Sie sollten aber in ihr Land zurückkehren,
um dort beim Wiederaufbau zu helfen, sobald es möglich sei!
Vernünftig. Es scheint mir ein fataler Fehler gewesen zu sein, die
Füchtlingsaufnahme damit zu begründen, dass man Arbeitskräfte in
Deutschland brauche.
30 Mai 2016
Der Prime Minister von Malaysia hat 600 (oder 900?) Millionen A$ auf
seinem Privatkonto aus Saudiarabien. Malaysia war bisher ein land mit
tolerantem Islam. Die Situation wird laufend weniger tolerant. Ist das
wohl verbunden mit der Geldüberweisung?
23 Mai 2016
Stimmt das? Wenn ja, gefährliches Abkommen. Die Verantwortlichen sollten
³gesackt² werden.
https://www.rt.com/news/343893-turkey-europe-qualified-refugees/
Auszug:
“During the same meeting, representatives of Germany, the Netherlands
and Luxembourg reportedly told the assembly that over the past weeks
Turkish authorities have repeatedly been rejecting exit applications
filed by Syrian well-trained engineers, doctors and other professionals,
who could successfully integrate into European societies.
Under
the controversial migrant deal, Brussels has given Ankara exclusive
rights to select refugees permitted to leave the country and re-settle
into the EU. Previously, the UNHCR, which was in charge of this
procedure, has been ³officially informed² by Turkish authorities that
Syrian academics will ³no longer be allowed to travel to Turkey,² Spiegel
wrote.”
23 Mai 2016
Sicherlich ist Russland kein Unschuldshase. Aber es geht ja vor allem
darum, eine gefährliche Eskalation zu vermeiden, von der Deutschland
besonders betroffen wäre wegen seiner exponierten Lage und den Atomwaffen
nahe einem dicht besiedelten Gebiet. In anderen Worten, ein starker
Kanzler oder eine starke Kanzlerin sollte alles in seiner/ihrer Macht tun,
um zu vermeiden dass sich Russland provoziert fühlt.
21Mai 2016
Und noch ein Punkt: Die USA halten es für fast selbstverständlich, dass
sie das Recht haben, in ihrer Nähe einzugreifen, wenn sie ihre Interessen
bedroht sieht, siehe die Kubakrisis und ihr Eingreifen in Granada. Die
Monroe-Doktrin! Und nicht nur in unmittelbarer Nähe, siehe die
Kolonisierung der Philippinen. Andere Staaten machen nur nach, was ihnen
vorgemacht worden ist.
21 Mai 2016
Vielen Dank. Was klar wird ist, dass sowohl in Georgien und in der Krim
Russland auf Aktionen reagierte, die es als gegen sich gerichtet sah. Der
³Westen² gab Georgien und der Ukraine moralische, mediale und militärische
Unterstützung, ohne dass man versuchte, Russlands Position zu verstehen.
Merkels Politik läuft in die gleiche Richtung. Wo bleibt die deutsche
Presse? Warum werden diese entscheidend wichtigen Probleme (Möglichmeit
eines Atomkrieges usw.) nicht mit dem Nachdruck diskutiert, die sie
verdienen? Und wo bleibt die deutsche Intelligenz, insbesondere Akademia?
Man schlittert, wie es scheint unaufhaltsam, einer Katastrophe entgegen.
In meiner früheren email hatte ich vergessen, einen weiteren ³Höhepunkt²
zu erwähnen: Israel hat sich erneut geweigert, einem diesmal von
Frankreich initiierten Ländertreffen beizutreten, um Frieden mit den
Palästinensern zu machen. Und Israel hat jetzt auch sein Antiraketensystem
von U-Booten aus getestet. Also: nicht Verhandlungen und Kompromisse,
sonder Militär!
19 Mai 2016
“Darauf verstaerke Russland seine
Truppen dort. Jetzt fand die NATO, dass diese Einheit nur fuer Kleinkrieg
stark genug ist. Regulaere russische Truppen wuerden sie ueberrollen,
bevor sie kampfbereit waere. Daher jetzt die 4 Bataillone oestliche der
Oder.” ——— Und zudem noch Raketenabwehr in Rumänien, angeblich um Europa
vor dem Iran zu schützen.
Und nicht zu vergessen, die sich zuspitzende Lage im Südchinesischen Meer,
und das grosse Fragezeichen Trump. Nicht unwahrscheinlich, dass er
amerikanischen Präsident wird. Will sich angeblich mit Putin und Kim
(Nordkorea) treffen, aber wie sieht er China?
Radical change in our approach to cut greenhouse gas emissions necessary
An article in Common Dreams:
Forget Paris, Scientists Say ‘Radical Change’ Only Way to Stay Below 2 Degrees
Forget Paris, Scientists Say ‘Radical Change’ Only Way to Stay Below 2 Degrees
Study by former IPCC chair comes amid rash of new research, all predicting the Earth will soon blow by key global warming thresholds
”
Global GHG emissions are not projected to decrease fast enough, even if all the pledges are fully implemented. Full implementation of the pledges will require the promised US$100 billion per year in financial assistance for developing countries to be realized. As a result, the 1.5°C target could be reached by the early 2030s and the 2°C target by 2050.
Further, the researchers minced no words when laying the blame for the missed targets on “political and sectoral interests,” including those “benefiting from the use of fossil fuels,” for promoting “deliberate misinformation” about the current situation.”
Trump on climate change
Donald Trump has repeatedly referred to climate change as a hoax
In today’s PBS news his views on climate change and his intention of how to deal (or not to deal) with it (withdrawal from the Paris accord, greater dependence on coal and oil) were contrasted with those of Hillary Clinton. It is clear that the consequences for climate change politics world-wide could be disastrous, if Trump was elected.
In previous posts of this blog and in the book edited by me: The Balance of Nature and Human Impact, Cambridge University Press 2013, the physics of climate change, ecological consequences and the politics of climate change, were discussed by some leading experts. There can be no doubt that human induced climate change is real and that urgent action to limit it is required. Trump’s views on some political aspects may well appeal to some in the electorate, but overriding everything should be the consideration that he could put civilization at risk if elected. He is only one of the many ‘leaders’ in several countries who put business interests before everything else (see https://krohde.wordpress.com/2016/02/27/misleading-information-on-climate-change-and-corrections/ ), but he would be the most dangerous one if elected, because he would head the country with the largest economy.
Arguments used by climate change sceptics and rebuttals
Hottest February on record
A few weeks ago I found a 16-page pamphlet in my mailbox titled: The Paris Climate Summit 2015. A waste? Hubris? Poor science? Alarmism gone mad? A gravy train? Take your pick.
A quote from the first page: ” But there is certainty beyond any doubt that CO2 is the building lock for all life on Earth and that without its presence in the global atmosphere at a sufficient concentration this would be a dead planet. Yet today our children and our public are taught that CO2 is a toxic pollutant that will destroy life and bring civilization to its knees”.
Also on page 1, Robert Mugabe, the “murderous tyrant”, is quoted as a speaker in favour of climate regulation: “Unless current trends are reversed, disaster stalks planet Earth”.
And in the Introduction: “Especially when one reads of the call for major changes to our economic and industrial systems …. on the basis of a theory which has been shown to have major flaws and errors. That’s right, let me repeat that “on the basis of a theory which has been shown to have major flaws and errors”.
What, then, is the present situation?
“NASA this weekend released new data which shows that February 2016 was not only the hottest in recorded history, but it soared past all previous records, prompting scientists to describe the announcement as “an ominous milestone in our march toward an ever-warmer planet.”
The average global surface temperature for February was 1.35°C warmer than the global average for the month between 1951-1980—a margin that shattered the previous record of 1.14°C, which was set just one month earlier—and exceeded preliminary figures released earlier this month.”
And Professor Stefan Rahmstorf, from the Potsdam Institute of Climate Impact Research, presently a visiting professorial fellow at the University of New South Wales, speaks of a kind of climate emergency. Full article here:
http://www.commondreams.org/news/2016/03/14/nasa-drops-major-bomb-march-toward-ever-warmer-planet
Of course, one observation does not prove a ‘theory’. Therefore, have a look here: https://krohde.wordpress.com/2016/02/27/misleading-information-on-climate-change-and-corrections/
Large-scale people movements in the Middle East not due to climate change alone
The large-scale movements of people from Syria, Iraq and Afghanistan to Europe are not the result of climate change alone but are due to complex interactions between various factors:
http://www.spiegel.de/wissenschaft/natur/loeste-klimawandel-den-syrien-krieg-aus-a-1077461.html
The German climate consortium (Deutsches Klima-Konsortium), including many German research institutes published a statement stressing that point
Climate dates about Syria show that the region warmed by about one degree over the last century. The serious drought 2006-2010 was the worst since the beginning of measurements at the beginning of the 20th century. About 1 1/2 million peasants lost their livelihood, and many moved to different parts of the country. The government cut subventions and introduced various other ‘liberal’ economic policies, which led to the disaster. Therefore, not climate change alone but the lack of adequate political measures must be held responsible.
Die Europakrise. Merkels Politik. Meine emails 1.2. -14.2.2016
14.2.1016
In der türkischen Region Aleppo bombardiert die Türkei kurdische Milizen
(nicht etwa die IS), und sie erwägt auch, gemeinsam mit Saudiarabien, den
Einsatz von Bodentruppen in Syrien (Spiegel online heute). Russland ist in
Syrien auf Einladung der legitimen syrischen Regierung (des Assad-Regimes
in westlicher Terminologie), Saudiarabien und die Türkei sind Aggressoren.
Wenn man sich also die heutige Konstellation ansieht: Deutschland
quasi-alliiert mit der Türkei und Saudiarabien, das letztere wohl das
rückständigste und autoritärste Regime im Nahen Osten. Die Türkei
mitverantwortlich für die Erfolge des IS (fast alle nichtsyrischen Kämpfer
des IS durch die Türkei eingeschleust, medizinische Betreuung von
IS-Kämpfern in der Türkei, Verfolgung von Akademikern und Journalisten,
die über die Unterstützung der Türkei für den IS berichten, Unterdrückung
der kurdischen Terrormilizen (in türkischer Terminologie), usw. — Russland
alliiert mit Syrien und dem Iran. Damaskus heute eine Stadt, in der
Aleviten, Sunnis, Shiiten und Christen usw. zusammenleben. Im Iran ein
weit liberalerer Islam als in den meisten anderen Ländern der Gegend. –
Wie mir scheint, liegt das primäre Interesse der Türkei darin, die Kurden
unten zu halten, die USA schienen von Anfang an vor allem darauf bedacht,
Russland unten zu halten. – So sehen es die Russen: Russland ist vom
Westen (sprich USA) im Stich gelassen worden, wie es auch gerade wieder in
München auf der Sicherheitskonferenz klar wurde.
Deutschland!?: völlig verfehlte Politik. Auch Frankreich hat ja gerade
erklärt, keine Flüchtlinge mehr aufzunehmen.
13.2.2016
Man liest dass Medvedev vor dem Ausbruch des dritten Weltkrieges warnt,
dass die NATO ihre Truppenpräsenz in Osteuropa erheblich erweitern will,
um den osteuropäischen Staaten grössere Sicherheit vor möglicher
russischer Aggression zu geben, amerikanische Politiker sprechen von einer
russischen Paranoia. Ist es sinnvoll, einem paranoiden Patienten zu
drohen? Merkel natürlich an der Vorfront der Russlandkritik, im Augenblick
wegen Russlands Syrienpolitik. Gauck, aus ähnlichem Holz geschnitzt,
deutet eine erneute Kandidatur an. Gott sei uns gnädig!
5.2.2016
Die Welt scheint mir zur Zeit die einsichtsreichsten Beiträge zum
Syrienkrieg zu bringen. Siehe hier:
http://www.welt.de/politik/ausland/article151861590/Saudi-Arabiens-Syrien-P
laene-bedrohen-die-ganze-Region.html
http://www.welt.de/debatte/kommentare/article151855936/Golfstaaten-sollen-s
penden-nicht-nur-Moscheen-bauen.html
1.2.2016
Vielen Dank. Man kann nur offen, dass der Kölner Karneval glatt abläuft.
Alles Gute!
Die sich entwickelnde Flüchtlingskrise in Europa. Flüchtlinge und Merkel, meine emails 5.1.- 31.1.2016
31.1.2016
……………………………………………………….. Hier in Australien (und sehr
wahrscheinlich weltweit) war das Fernsehen und Zeitungsberichte voll nicht
nur von Merkels Reden und Bemerkungen, sondern auch von Aufnahmen von
‘Empfangskommittees’, die zum Teil mit Kerzen, Spielzeug für Kinder usw.
die Flüchtlinge willkommen hiessen. Natürlich sehr schön und emotional,
aber sehr wahrscheinlich auch ein Anreiz für mehr Flüchtlinge zu kommen.
Daher: konnte man wirklich kurzfristige Reaktionen (Anstieg der
Flüchtlingszahlen) erwarten, oder kann der Effekt vielleicht eine
Tendenzstärkung gewesen sein, d.h. ist es möglich, dass ohne Merkels
Bemerkungen und die Reaktionen darauf ein Abflachen der Kurve erfolgt wäre
(immerhin 100000 oder so über ein Jahr weniger)?
Merkels (und der EU) hauptsächliche Fehlleistung scheint mir darin zu
liegen, dass man zwar davon redet, die Ursachen der Flüchtlingskrise zu
bekämpfen, aber nichts Ernsthaftes tut. Mehr Waffen an Saudiarabien, und
Stützung in der Türkei eines Regimes, das kaum an einer wirklichen
Entspannung interessiert ist, welches die Grossmachtträume Erdogan’s nicht
befriedigt,um nur zwei Beispiele zu nennen. Man hat sich in eine Situation
manövriert, in der man sich Erdogan sozusagen ausliefert und die Gefahr läuft, in eine
Konfrontation mit Russland hineingezogen zu werden. Erdogan, der Reden in Deutschland
hielt, wo er Türkischstämmige dazu aufrief, sich zwar zu integrieren aber nicht zu
assimilieren, Erdogan, der Journalisten und Akademiker verfolgt, die davon
berichten, wie die Türkei die IS in Syrien aktiv unterstützt! Erdogan, der
nichts besseres zu tun hat, Russland durch den Abschuss eines russischen
Jets zu provozieren. Merkel will das honorieren, indem man
Aufnahmegespräche in die EU forcieren will. Ist das klug?
Having said that, Professor Colliers Bemerkungen (die ich nur aus Deiner
email kenne), dass Merkel an allem Schuld sei, ist natürlich wie üblich in
weiten deutschen (und nicht nur Akademiker-) Kreisen, die sich selten
zurückhaltn, wenn es an Schuldzuweisungen an Deutschland geht, kaum
akzeptabel. Immerhin hat sie menschlich reagiert. Und vielleicht sollte man sich so
etwas bei Politikern auch anderer Länder wünschen. Das Gegenteil, wie hier
in Australien betieben, ist wohl kaum nachahmungswert.
29.1.2016
Gut, sich ab und zu einmal an die Motive der Politik verschiedener
westlicher Länder zu erinnern.
http://www.spiegel.de/einestages/kongo-der-mord-an-patrice-lumumba-1961-a-1
074116.html
24.1.2016
Das verstehe ich nicht. Meinst Du dass Deutschland 8 Millionen Flüchtlinge
aufnehmen soll? Der Vergleich mit Jordanien und Libanon scheint mir zu
hinken. Immerhin ind diese Länder kulturell und vor allem in der Religion
den Herkunftsländern viel ähnlicher.
20.1.016
Germany: Asylum Seekers Make Demands
by Soeren Kern
October 23, 2015 at 5:00 am
http://www.gatestoneinstitute.org/6753/germany-migrants-demands
17.1.2016
Australien: das ist nur die Spitze des Eiberges. Es kam auch zu brutalen
Angriffen von Wachmannschaften auf Flüchtlinge auf Manaus-Island mit
tödlichem Ausgang, und Angestellten inklusive medizinischem Stab ist es
untersagt, über die Zustande in den Lagern zu berichten. Zuwiderhandlungen
können mit bis zu zwei Jahren Haft bestraft werden.
Deutschland: was erwartet man eigentlich, wenn hunderttausende
alleinstehende Männer ins Land gelassen werden?
16.1.2016
Die Nachricht, dass Flüchtlinge in deutschen Schwimmbädern Frauen
belästigen, hat hier für einiges Aufsehen gesorgt.
Aber wie sieht es in Australien aus?
“Self-harm in detention centres at epidemic levels, internal documents show
Sydney Morning Herald January 16, 2016
‘Incident logs from the Department of Immigration and Border
Protection covering one year, obtained under freedom of information
laws, paint a picture of depression, desperation and violence at
Australia’s domestic and overseas detention camps and in the community.
They raise fresh questions over the human rights
implications of Australia’s tough border protection regime, which has
been condemned by the United Nations, and will fuel calls for children
to be immediately released from detention.
The data shows that in the year to July 2015 there were 188 incidents of self-harm
involving asylum seekers at Nauru, about one every two days. There
were 55 such self-harm acts at Papua New Guinea’s Manus Island.
Scars on the torso of Mohammad Albederee,
who has been cutting himself with a razor.
They included detainees swallowing poisons, stuffing tea
bags down their throats and hanging by bed sheets or other makeshift
nooses.
In one incident on Manus Island a
detainee “inflicted 12 lacerations to his stomach with a razor
blade”. In another, a man “swallowed a Christian cross pulled from his
wallet”.
Another man was found attempting to damage his
wrist “with a small ring of metal” and was restrained. He tried to
break free, saying, “I want to die, let me die.”
Mohammad Albederee has been cutting
himself with a razor.
At Nauru in October 2014 a detainee, apparently upset
after meeting his lawyer, “wrapped himself in toilet paper and attempted
to get hold of a lighter”. In another incident, a woman “poured boiling
water over [her] lower limbs”.
Also at Nauru, a man “was seen to jump from a top bunk with [a] torn sheet around his neck”,
while, separately, a detainee who swallowed anti-dandruff shampoo “was
on the floor of the tent vomiting and … appeared to be unconscious”.
In May last year a man had “sewn a heart shape design into his hand using
[a] needle and thread”. The rate of self-harm is even higher in Australia’s onshore detention
network, where there were 706 acts in 12 months – almost two incidents a day. They includedasylum seekers living in the community or in community detention.”
Read more:
http://www.smh.com.au/federal-politics/political-news/selfharm-in-detention
-centres-at-epidemic-levels-internal-documents-show-20160115-gm74q3.html#ix
zz3xNFlCwos
13.1.2016
Ich hatte vergessen: wie man liest, ist zumindest ein deutscher Pfarrer
aktiv, Asylanten zum Christentum zu bekehren. Sprengstoff!
13.1.2016
Gestern habe ich zufällig die polnischen Nachrichten (1/2 Stunde, auf
polnisch) Im Fernsehen gesehen. Deutschland prominent: deutscher
Botschafter in Warschau vorbestellt, um angeblich antipolnische
Bemerkungen deutscher Politiker zu erklären (ich verstehe polnisch zwar
nicht, aber konnte den Nachrichten folgen, weil mir die Geschichten schon
bekannt waren); Uebergriffe vor dem Kölner Hauptbahnhof; VW-Skandal; Sieg
der polnischen Volleyball-Mannschaft über Deutschland! Von anderer Seite
hört man, dass gewisse Kreisen Polen nicht mehr von Deutschland sprechen,
sondern vom Reich. Kongruent mit Marine LePen: Merkel die Kaiserin
Europas! Die Rechten finden sich zusammen, auch weltweit: The Australian
(Murdoch) seitenlange Berichte über Köln.
Und was würde wohl in Deutschland passieren, wenn irgendwo am
Brandenburger Tor ein Selbstmordattentäter ein Dutzend Leute mit in den
Tod risse, wie grade in Istanbul passiert? Die von der deutschen Koalition
angekündigten Gesetzesänderungen, die ein schnelleres und leichteres
Abschieben von straffälligen Asylanten vorsehen, dringend notwendig! Vor
allem aber: effektive Kontrollen der europäischen Grenzen!
11.1.2016
Der deutsche Justizminister hat erklärt, dass die Übergriffe in Köln und
anderen Städten “abgestimmt oder vorbereitet” gewesen seien. Natürlich
möglich, oder ist das nur ein Ausdruck der Inkompetenz verstehen zu wollen, dass die Bedingungen
derartige Vorfälle mehr oder weniger unausweichlich machen. Abgestimmt in
dem Sinne, wie Kochtöpfe abgestimmt sind, die zur gleichen Zeit zum Kochen
kommen, wenn sie etwa gleicher Grösse sind, gleiche Wassermengen enthalten
und auf der gleichen Kochplatte stehen. In anderen Worten: nicht abgestimmt oder vorbereitet,
sondern inkompetente Politik. Aber mir scheint wie gesagt, wir wissen es (noch) nicht.
9.1.2016
Ein Artikel in Christian Today (9.1.16), dem grössten “christlichen”
online News Magazin in Australien.
“Muslim refugees run amuck, rape German women; police told by officials to
cover up crime to avoid panic”
http://www.christiantoday.com/article/muslim.refugees.run.amuck.rape.german
.women.police.told.by.officials.to.cover.up.crime.to.avoid.panic/76004.htm
8.1.2016
Was in Deutschland zu fehlen scheint, ist common sense.
Nicht verwunderlich, wenn man bedenkt, dass das deutsche Äquivalent
gesunder Menschenverstand heisst. Viel zu lang!
Jetzt werden die Ausmasse der Silvester-Übergriffe so allmählich klar,
nicht nur in Köln, sondern auch in anderen Großstädten, und man wundert
sich, wie so etwas passieren konnte. Anscheinend ist es noch niemand
aufgefallen, dass einige hunderttausend junge Männer alleine nach
Deutschland gekommen sind (etwa ein Drittel der über eine Million
Asylanten). Canada will 25000 Flüchtlinge aufnehmen, aber keine
alleinstehenden Männer! Völliges Fehlen des gesunden Menschenverstandes in
der Asylpolitik in Deutschland.
5.1.2016
“Die Reaktion gegen Saudi-Arabien ist von seiten des Irans ziemlich
scheinheilig, da auch dort massenhaft Todesurteile und Exekutionen
geschehen.²
Ich weiss nicht: immerhin scheint mir die Hinrichtung eines sehr
prominenten Schiitenpredigers zu diesem Zeitpunkt (Angriffe im Jemen usw.)
eine gewollte Provokation zu sein. Reaktionen in Teheran schienen spontan
zu sein.
Ich hatte vergessen: Erdogan hat ja Hitler öffentlich als eine Art Vorbild
gepriesen (obwohl später etwas heruntergespielt).
Die sich entwickelnde Flüchtlingskrise in Europa. Flüchtlinge und Merkel, meine emails 23.7.2015 -4.1.2016
4.1.2016
So, Saudiarabien ‘hat die Macht mit dem Schwert erobert und wird sie mit
dem Schwert verteidigen’ (Der König von Saudi-Arabien, so ungefähr). Und um
das ganz klarzumachen, hat es eine Massenexekution von über 40
‘Aufrührern’, d.h., Leuten, die nicht mit der Monarchie zufrieden sind,
durchgeführt, darunter ein prominenter Schiitenprediger. Die Reaktion,
unter anderem vom Iran, war voraussehbar. Das ganze, ebenso wie die
Invasion des Jemens durch die von Saudiarabien geführte Koalition,
anscheinend ganz bewusst herbeigeführt, um die Lage im Nahen Osten zu
destabilisieren. Und woher bezieht Saudiarabien seine Waffen? Zu einem
grossen Teil aus Deutschland. — Zur gleichen Zeit eskalierende Gewalt
Erdogans gegen die Kurden (und wer sitzt mit Türken in den Flugzeugen?
Anscheinend Deutsche, allerdings nicht in Flugzeugen die Angriffe gegen
Kurden fliegen).
Eine Zwischenbilanz von Merkels Politik: sehr eindrucksvolle Rede zum
Neujahr (“wir schaffen das”), aber auch drastischer Rechtsruck in der EU,
indirekt oder direkt auf die offene Asylpolitik zurückzuführen
(Frankreich: Front Nationale; Polen: Angriffe der Rechtsregierung auf die
Unabhängigkeit der Medien und der Justiz, usw.).Vielleicht hätte die
Rechte in Polen die absolute Mehrheit ohne den Massenandrang von
Flüchtlingen nicht gewonnen, vielleicht hätte Erdogan die absolute
Mehrheit in der Türkei ohne die Wahlhilfe Merkels (durch ihren Besuch in
der Türkei während des Wahlkampfes) nicht gewonnen.
Wie will man die Massenwanderung aus Syrien, Iraq usw. stoppen, wenn man
nichts gegen die Ursachen unternimmt,und die liegen meines Erachtens in
Saudiarabien (fundamentaler Islam) und Israel (Unterdrückung der Moslems).
Wie ich bereits früher sagte: keine U-Boote an Israel, keine Panzer an
Saudiarabien.
3.12.1015
Die Welt online heute, wie mir scheint, haargenau getroffen (was soll der
Unsinn, Soldaten nach Syrien zu schicken, wenn man die eigentliche Ursache
ignoriert):
http://www.welt.de/debatte/kommentare/article149537626/Die-groessten-Brands
tifter-in-Nahost-kommen-aus-Riad.html
“Die größten Brandstifter in Nahost kommen aus Riad
Die Expertise des BND über Saudi-Arabien sollte uns alarmieren. Wir
paktieren mit einem mittelalterlichen Regime, das Mörderbanden in alle
Welt entsendet und einen Krieg gegen die eigene Jugend führt.
“Saudi-Arabien muss heute
mit dafür verantwortlich gemacht werden, das Monster IS erschaffen zu
haben. Denn im ideologischen Streit mit der anderen Regionalmacht Iran
um Hegemonie zwischen Golf und Mittelmeer war und ist Riad beinahe jedes
Mittel und jeder Helfershelfer recht, sofern er sunnitischer und nicht
schiitischer Glaubensrichtung ist: Taliban, al-Qaida, IS.
Nihilistische Mörderbande Saudi-Arabien
und Katar sind über die klandestinen Kanäle von Stiftungen,
Moscheevereinen und privaten Zuwendungen die größten Sponsoren der
nihilistischen Mörderbande IS, mit der sich die fundamentalistischen
Kreise in den Golfmonarchien allen Ernstes noch immer im selben Boot
wähnen. Dabei ist längst deutlich geworden, was Salafisten und
Wahhabiten bei allen ideologischen Übereinstimmungen fundamental
voneinander unterscheidet: Das saudische Herrscherhaus der al-Saud ist
eine irdische, eine menschliche Macht, die der IS ablehnt und bekämpft.”
Und noch einmal: Deutschland hat sich in eine Lage manövriert, in der es
sich aus Loylalität gegenüber Frankreich verpflichtet fühlt, in Syrien
militärisch mitzumachen, wie seinerzeit Wilhelm II gegenüber Österreich
-Ungarn. Hollande’s Motive? (wahrscheinlich zumindest ist es, dass sich
seine Umfragewerte und Wahlaussichten wegen der so ostentativ gezeigten
‘Stärke’ verbessern). Frankreich hat als erstes Land die IS als Staat
praktisch anerkannt, und spielt damit in die Hände der IS.
30.11.2015
Ich habe gerade in der Deutschen Welle ein Interview mit dem
Fraktionsvorsitzenden der Linken, Dietmar Bartsch (?) gesehen. Das
Vernünftigste, dass ich bisher zum Syrieneinsatz gehört oder gesehen habe
habe: Unterstützung Frankreichs ja, aber nicht militärisch. Das Beispiel
Afghanistan habe gezeigt, dass eine militärische Lösung nicht möglich sei.
Unterstützung der Kurden, Drosselung der Waffenexporte nach Saudiarabien
und in die Golfstaaten ja. Weltweite Lösung der Terrorgefahr: mehr soziale
Gerechtigkeit und Offenheit der Gesellschaft.
Nach der Interviewerin: Wagenknecht hat darauf hingewiesen, dass ein
deutscher militärischer Einsatz in Syrien die Gefahr von Terroranschlägen
in Deutschland erhöhe.
29.11.2015
Heute im Spiegel online:
http://www.spiegel.de/politik/ausland/ex-us-geheimdienstchef-mike-flynn-ueb
er-den-is-wir-waren-zu-dumm-a-1065038.html
“Ex-US-Geheimdienstchef über den IS: “Wir waren zu dumm”
“SPIEGEL ONLINE: Den IS gäbe es nicht, wenn die Amerikaner nicht 2003 in
Bagdad eingefallen wären. Bedauern Sie..
Flynn:ja, absolut
SPIEGEL ONLINE: den Irakkrieg?
Flynn: Das war ein riesiger Fehler. So brutal Saddam Hussein war –
ihn nur zu eliminieren, war falsch. Das Gleiche gilt für Gaddafi und
Libyen, das heute ein failed state ist. Die große historische Lektion
lautet, dass es eine strategisch unglaublich schlechte Entscheidung war,
in den Irak einzumarschieren. Die Geschichte sollte und wird über diese
Entscheidung kein mildes Urteil fällen.”
28.11.2015
Wie man hört, hat die neue polnische Regierung (die möglicherweise auch
wegen der Flüchtlingskrise zur Macht kam) als eine ihrer ersten Massnahmen
alle Euroflaggen herunternehmen lassen. Jetzt gilt wieder nur Polen.
Ebenfalls, die polnische Regierung will ihre Flüchtlingspolitik nach
derjenigen Ungarns ausrichten. Welcome to Euroland!
Erdogan hat Russland gedroht, den Abschuss des russischen Flugzeuges (und
eines Hubschraubers) nicht als VorWand zur Verschärfung der Lage zu
benutzen. Wer ist hier wohl der Scharfmacher? Anscheinend fühlt sich
Erdogan als Mitglied der Nato abgedeckt (Sarajevo, Serbien und Russland
vor dem ersten Weltkrieg????). Und Deutschland unter Merkel hat sich aus
Loyalität mit Frankreich entschlossen, Flugzeuge und eine Frigatte nach
Syrien zu schicken. Ist all das wirklich eine geeignete Reaktion auf die
Anschläge in Frankreich? Die Linken in Deutschland und der linke Flügel
der Labourparty in GB scheinen mir zur Zeit die einzigen vernünftigen
Leute zu sein. Wie ein Linker (oder Labourman?) sagte: hat man denn immer
noch nichts aus Afghanistan gelernt?
28.11.2015
Jetzt haben wir also eine Situation in welcher Marie Le Pen Angela Merkel
wegen ihrer Flüchtlingspolitik als Kaiserin Europas bezeichnet. Unsere
Angela hat sich immer noch nicht dazu durchgerungen, eine Obergrenze für
die Flüchtlingsaufnahme zu setzen, und sie will osteuropäische Länder, die
sich weigern, Flüchtlinge aufzunehmen, zahlen lassen. Sie hat Erdogan
praktisch in seinem Wahlkampf unterstützt, indem sie die Türkei während
des Wahlkampfes besuchte, und ihm zugesichert, die EU-Aufnahmegespräche zu
beschleunigen und die Visaregelungen zu entschärfen: den Erdogan, der
mit Vorrang nicht die IS sondern die Kurden bekämpft, der kürzlich ein
Russisches Kampfflugzeug abschiessen liess, weil es angeblich 17 Sekunden
in den türkischen Luftraum eingedrungen war (in diesem Zusammenhang, als
vor
Jahren ein türkisches Flugzeug von der syrischen Luftwaffe abgeschossen
worden war, sagte er, ein kurzes versehentliches Eindringen in einen
fremden Luftraum sei kein Grund zum Abschuss). Den Erdogan, der kürzlich
zwei Journalisten verhaften lies, weil sie über die Lieferung von Waffen
durch die Türkei an Rebellengruppen in Syrien berichtet hatten.
Hollande war jetzt in Moskau, um ein gemeinsames Vorgehen mit Russland
gegen die IS zu beschliessen. Er schliesst auch eine Zusammenarbeit mit
Assad nicht aus (was übrigens auch durch die neue australische Regierung
nicht ausgeschlossen wird). Die Deutschen sind da zurückhaltender, man hat
ja seine Prinzipien: (Der Spiegel heute über die Zusammmenarbeit gegen
die IS “…..Doch es gibt dabei eine Menge Hürden – bis hin zur
Möglichkeit, mit Diktator Assad kooperieren zu müssen”). Merkel riskiert,
in die Isolierung gedrängt zu werden!
Marie Le Pen hat vergessen zu erwähnen, das die Kaiserin keine Kleider
hat: Lufthansa-Debakel, Deutsche Bank-Debakel, Volkswagen-Debakel,
misslungene Ukraine- und Flüchtlingspolitik. Aber immerhin, wir haben ja
einen Präsidenten, der der Welt Moralpredigten gibt (wie es schon Erdogan
seinerzeit merkte und kommentierte, als Gauck die Türkei besuchte), die
die Welt aber mit Sicherheit ignorieren wird. Bei seinem USA-Besuch
strahlenden Auges und dankbar, endlich oben (im Weissen Haus) angelangt zu
sein, aber mit ernster Miene den besuchenden vietnamesischen Präsidenten
in Berlin auf die Notwendigkeit, die menschlichen Freiheiten in Vietnam zu
verbessern, hinweisend.
Über Putin und Erdogan siehe auch hier:
http://www.theguardian.com/world/2015/nov/26/russia-turkey-jet-mark-galeott
i
11.2015
Kurzfristig gesehen scheinen mir die grössten Gefahren zu sein, dass es zu
Ausfällen gegen Flüchtlinge kommt, und dass jeder, der sich kritisch zur
Flüchtlingspolitik der Regierung äussert, als Neonazi verschrieen wird.</strong> In
die Richtung des letzteren scheint mir die Reaktion auf Erika Steinbachs
Tweet zu gehen:
Sarrazin wird weitgehend totgeschwiegen (obwohl viele sein Buch nicht
gelesen haben), soll man auch Helmuth Schmidt totschweigen:
Aus der Berliner Zeitung 11.11.15.
“Als pietätlos
und schockierend empfanden viele den Tweet, den die stellvertretende
Vorsitzende der CDU/CSU-Bundestagsfraktion am Nachmittag postete.
„Altkanzler Helmut Schmidt ist tot. Wir haben in unserer
Fraktionssitzung seiner in Respekt gedacht,“ twitterte Steinbach in
Kombination mit einem Zitat des gestorbenen Politikers: „Wir können
nicht mehr Ausländer verdauen, das gibt Mord und Totschlag“.
11.11.2015
Vielen Dank. Im Ausland wird das weitgehend so gesehen: Merkel ist durch
ihre zu weit offenen Arme im grossen Masse verantwortlich. ‘Wir schaffen
das’, ‘selbstverständlich sind Flüchtlinge bei uns willkommen’,
Fernsehaufzeichnungen darüber, wie Flüchtlinge an der Grenze und später in
Berlin und in anderen Städten herzlich willkommen geheissen werden. So
etwas spricht sich im Zeitalter der sozialen Media und des Fernsehens usw.
sehr schnell herum, und so hat dies alles natürlich zu der
Flüchtlingswelle beigetragen, in welchem Ausmass muss allerdings fraglich
sein, und ob Merkel das gewollt hat oder nicht. Vielleicht wären alle
sowieso gekommen.
Übrigens auch in Deutschland scheinen viele ja Merkel für verantwortlich
zu halten. Ein Auszug aus eine email, die ich gerade erhalten habe:
“Vielleicht hat der Winter Mitleid mit den Tausenden von Flüchtlingen in
hier in Deutschland. Eine Katastrophe, die die Merkel da angerichtet hat,
vor allem, wenn die gesamten Familienmitglieder nachgeholt werden. In
Havelberg sind bisher 40 minderjährige Syrer und Afghanen aufgenommen. Sie
werden hier mit grosser Skepsis beobachtet.’
Deutsche Welle, Nachrichten vor zwei oder drei Tagen: lange Sendung über
den VW-Skandal, lange Sendung über die ‘gekauften’ Weltmeisterschaften im
Fussball, und um alles abzurunden, lange Sendung über die ‘unerwartet’
grosse Zahl von Exnazis in Bundes- und DDR-deutschen Ministerien in den
Nachkriegsjahren, kürzlich von einem Institut in Potsdam dokumentiert. Die
ersten beiden Punkte OK, aber hat man denn nichts besseres zu tun, als der
Welt klarzumachen, wie schlecht die Deutschen waren und sind, sechzig
Jahre später. Haben die Esel Globke und Kiesinger vergessen? Und haben sie
vergessen, dass auch die Russen und Amerikaner Exnazis herzlich
willkommmen hiessen, sofern sie zum Raketen, secret service usw. -Programm
beitrugen?
7.11.2015
Afghanistan lag wohl etwas anders,die USA unterstützten die muslimischen
“Freiheitskämpfer” gegen die Sowjetunion (später gemausert zu Taliban und
El Quaida), in Syrien sollten beide (USA und Russland) aber ähnliche
Interessen haben (zumindest kann man nur hoffen, dass sowohl Russland wie
die USA das auch so sehen). Die vernünftige Politik schein mir zu sein,
die legitime syrische Regierung, die auch von der UN als solche anerkannt,
ist zu unterstützen, wie es Russland schon immer tat.
Flüchtlingskrise: man kann nur hoffen, dass das gut geht. Angela Merkel
scheint sich erheblich übernommen zu haben. Wie mir ein Freund schrieb:
auf einer Gratwanderung. Im schlimmsten Fall: Spaltung Europas (und
vielleicht sogar der Bundesrepublik: Bayern und “Preussen”), starker
Rechtsruck, Ausfälle gegen Asylanten. Viele halten es für
unverantwortlich, solche Massen unkontrolliert ins Land zu lassen
(Infektionskrankheiten, Salafisten und IS), die wohl alle kaum integriert
werden können und wahrscheinlich auch nicht integriert werden wollen.
10.2015
Danke. Wir gehen gefährlichen Zeiten entgegen, vor allem falls die
Republikaner an die Macht kommen. Hattest Du wirklich ernsthaft gehofft,
dass die Amerikaner den Russen ein von Dir vorgeschlagenes Angebot gemacht
hätten? Merkel sollte etwas übernehmen, aber sie hat ja bereits in der
Ukraine-Krise wie mir scheint nicht das getan, was getan hätte werden
sollen (obwohl sie das schlimmste vielleicht verhindert hat), und ebenso
in der Flüchtlingskrise (siehe Anlagen: The Australian 24.9.15). Die Idee,
dass Deutschland Millionen von Flüchtlingen als Arbeitskräfte braucht, ist
wohl deutlich unwahrscheinlicher geworden (VW-Skandal), und was macht man
dann?
19.9.2015
On the way to armageddon!!??
http://www.commondreams.org/views/2015/09/18/republican-foreign-policy-cons
ensus-lunacy
Der letzte Satz des Artikels:
“There is a dangerous vacuum on foreign policy a vacuum caused by the
withdrawal of common sense and prudence, and filled with unhinged
bluster and blind belief in the military. Listening to Republicans, one
can only shudder at the fate of our country.”
Sollte Deutschland, die EU usw. fortfahren, sich so eng an die USA zu
binden?
14.9.2015
Vor ein paar Tang hatten wir Besuch von Mr. und Mrs. Watt, ursprünglich
aus Sri Lanka, lange in Nordindien, er Ingenieur, sie viele Jahre lang
Sekretärin in der Zoologie, Armidale, wo sie viele meiner Arbeiten und
Briefe tippte. Wird Dich kaum interessieren, jedoch dies vielleicht: Vor
etwa 25 oder 30 Jahren sagte er mir, dass Deutschland sich lächerlich
mache (in Sri Lanka anscheinend). Wenn jemand nach Deutschland wolle,
schiffte oder buchte er/sie sich, ein, warf den Pass weg und beantragte
Asyl in Deutschland, meist mit Erfolg.Ich weiss nicht, ob das tatsächlich
möglich war, aber es zeigt zumindest, was man schon damals in Teilen
Asiens so dachte.
12.9.2015
Sicherlich. Jedoch gibt es einen entscheidenden Unterschied: die jetzt
kommenden Flüchtlinge gehören einer anderen Kultur (und weitgehend
Religion) an und die Frage erhebt sich, wie weit sie sich eingliedern
lassen. Man muss also hoffen!
9.9.2015
In meiner letzten email schrieb ich, dass Saudi-Arabien usw keine
Flüchtlinge aus Syrien aufnehmen. Aber immerhin, wenn die Bildzeitung
Recht hat, haben sie angeboten, den Bau von 200 Moscheen in Deutschland zu
finanzieren. Das führt zu der Frage, inwiefern die ganze Situation nicht
geplant ist: Moslemisierung von Deutschland. Erdogan, Saudi-Arabien, die
Emirate, die IS sozusagen Hand in Hand.
Schuldgefühle sind auf lange Sicht keine solide Grundlage für eine
rationelle Politik.
9.9.2015
Und nicht zu vergessen: die Rolle der Türkei, Saudi-Arabiens und der
Golfstaaten. Warum kommen plötzlich so viele Flüchtlinge aus der Türkei?
Ist das gesteuert? Warum nehmen Saudiarabien und die Golfstaaten keine
Flüchtlinge auf? All diese Staaten sind enge Verbündete der USA, doch die
Türkei bombardiert vorwiegend die Kurden und nicht die IS, und die anderen
bombardieren gerade den Yemen in Schutt und Asche, aber nicht die IS.
9.9.2015
Was die australische Flüchtlingspolitik anbetrifft, ist sie völlig
unmoralisch. Sie wurde von den Liberalen installiert, um Wählerstimmen zu
gewinnen: man spielte die Furcht vor illegalen Einsanderen bewusst hoch.
Man setzte die Füchtlinge in Rettungsboote und überliess sie ihrem
Schicksal, oder bezahlte Schmuggler, die Schiffe mit den Flüchtlingen nach
Indonesien zurückzubringen. Diejenigen, die es nach Australien geschafft
hatten, wurden nach Manaus-Island in Papua-Neuguinea, und nach Nauru im
Pazifik, praktisch in Konzentrationslager, gebracht. Es ist strafbar, über
die Zustände dort zu berichten, und eine Grüne Senatorin, die sich vor Ort
informieren wollte, wurde selbst auf der Toilette mit Kameras überwacht.
Trotz alledem ist durchgesickert, dass es zu Vergewaltigungen,
Kindermisshandlungen und selbst einem Mord gekommen ist. Das alles aus
humanen Gründen gemacht wurde, ist ein “spin”, der nachträglich erfunden
wurde, um den Leuten das Gefühl der moralischen Überlegenheit zu geben.
Man hat auch mehr als 50 Millionen A$ investiert um vier Flüchtlinge nach
Cambodia zu schicken, um den “Erfolg” der Politik zu demonstrieren.
Cambodia, ein Land das nicht einmal die primitivsten rechtliche
Schutzmassnahmen garantieren kann. Man hat auch Tamilen nach Sri Lanka
zurückgeschickt und afghanische Minderheiten nach Afghanistan, obwohl man
wusste, dass sie dort in Lebensgefahr sein würden. – Abbott ist ein
quasifaschistisches SŠ, kaum zur Nachahmung empfohlen, vor allem da man in
Deutschland ja derartiges aus er Vergangenheit kennt.——- Man
diskutiert zur Zeit, ob man vielleicht 10000 Flüchtlinge aus dem Nahen
Osten aufnehmen soll, aber vor allem oder ausschließlich Christen.
Was Europa anbetrifft, sieht die Situation ganz anders aus, vor allem
wegen der enormen Zahlen potentieller Flüchtlinge und den so nahen
Quellen. Hier eine konsequente Politik der überwachten Rücksendung der
Boote nach Nordafrika zu erwägen, wird sich auf die Dauer kaum vermeiden
lassen. Ob Merkels Politik richtig oder falsch war, wird die nahe Zukunft
zeigen. Ist sie sustainable??
Um noch einmal auf Australien zurückzukommen, die USA, Grossbritannien und
Australien sind primär für die Situation verantwortlich, durch den Sturz
Saddam Husseins, und Frankreich ebenfalls für den Sturz Gaddafis. Im Iraq
vor der Invasion bestand ein relativ fortschrittliches Land mit gut
entwickeltem Erziehungs- und Gesundheitssystem und Schutz der
Minderheiten.Immerhin war ja selbst der Vizepräsident ein Christ. Diese
Länder (und Frankreich wegen der führenden Rolle in der Destabilisierung
Syriens und Libyens) sollten auch eine führende Rolle in der Aufarbeitung
der Konsequenzen übernehmen. Fromme Hoffnung! Was man will, ist mehr
Bombardierungen, ohne sich um die Erfolgschancen und die Konsequenzen im
Klaren zu sein.
So viel für heute. Ob Dein Kalkül die derzeitige Politik rechtfertigt,
scheint mir zumindest fraglich zu sein. Nicht nur Quantitäten , sondern
Qualitäten (Religion, Anpassungswille usw. usw) sind wichtig,und vor alle
auch die Schnelle der Einwanderung und der Aufnahmewille der deutschen
Bevölkerung. Siehe meine letzte email.
27.8.2015
Die Fragen erheben sich natürlich, ob man die qualitativen Aspekte
(Religion, Qualifizierung, Wille zur Assimilierung usw.) ignorieren darf,
und ob die sehr schnelle Einwanderung von vor allem kleineren Gemeinden
“verdaut” werden kann. Wenn nicht, darf man wohl erhebliche soziale
Unruhen erwarten. Ferner, braucht Deutschland tatsächlich so viele
Einwanderer, da die sich schnell entwickelnde Technik ja viele
Arbeitsplätze überflüssig macht. Und ebenfalls nicht zu vergessen, die
TV-Bilder scheinen wohl zu zeigen, dass es sich bei vielen Asylanten nicht
um echte politische Flüchtlinge sondern um Leute handelt, die ein besseres
Leben wollen. Und was passiert, wenn die wirtschaftliche Lage in
Deutschland sich zum Schlechteren ändert?
26.8.2015
In Europa und vor allem auch Deutschland scheint es ja im Augenblick
munter zuzugehen. Wie siehst Du die Situation bezüglich der Massen von
Asylanten? In Australien wurden Wahlen wegen ein paar Flüchtlingen, die
per Boot kamen, verloren und gewonnen, und man sperrt diejenigen, deren
Boote nicht einfach nach Indonesien zurückgeschickt wurden und die es
tatsächlich nach Australien schafften, unter unwürdigen Umständen auf
Inseln ein, ohne Recht auf Aufnahmen in Australien.
23.7.2015
Noam Chomsky hat sich in einem Interview (meine Version im ‘Freitag’) über
wichtige aktuelle Probleme geäussert, u.a.über den Klimawandel,
Iran/USA/Israel, Griechenland. Du kennst seine Meinungen wahrscheinlich
schon, aber hier ist ein link:
https://blog.une.edu.au/klausrohde/2015/07/23/noam-chomsky-uber-den-klimawan
del-und-die-zukunft-des-intelligenten-lebens-auf-der-erde/
Natürlich hält er sich nicht zurück, seine Meinung völlig unbehindert von
historischen Schuldgefühlen (die er ja nicht hat) zu äussern.In
Deutschland wohl praktisch unmöglich.
Free book on parasites in aquaculture
Entire book, with many colour and black/white figures, “Negative Effects of Parasites on Fish Farms Production”can be downloaded here:
Contents:
Trypanosomosis, cryptobiosis, Ichthyobodosis
Is there a role for philosophy in science?
Scientists who adhere to a strictly “naturalistic” interpretation of science claim that only approaches which can be tested empirically (verified and/or falsified) are valid. The nobel laureate in physics Richard Feynman, for example, argued that string theory was not testable and therefore not scientific. A number of physicists and philosophers of science recently met in Munich to discuss the problems which have arisen in physics because theories, such as string theory, become increasingly more difficult to test. Some theoreticians at the meeting provided arguments to show that philosophical approaches, which in the foreseeable future (if at all) cannot be tested empirically, might well be valid.
For a full discussion see here:
“String theory, the multiverse and other ideas of modern physics are potentially untestable. At a historic meeting in Munich, scientists and philosophers asked: should we trust them anyway?”
New book on the physics of climate change
A new book on the physics of climate change by the distinguished climate physicists Michael Box and Gail Box of the University of New South Wales has just been published by CRC Press: Physics of Radiation and Climate.
For details see here:
https://www.crcpress.com/Physics-of-Radiation-and-Climate/Box-Box/9781466572058
UN Human Rights Investigator delays visit to Australian refugee centres
According to the ABC 27.9.15,
‘The United Nations special rapporteur on the human rights of migrants has postponed a planned trip to Australia, claiming the Federal Government’s immigration legislation preventing people talking about what happens in detention facilities does not allow him to carry out his job.’
“In preparing for my visit, it came to my attention that the 2015 Border Force Act, which sanctions detention centre service providers who disclose ‘protected information’ with a two-year court sentence, would have an impact on my visit as it serves to discourage people from fully disclosing information relevant to my mandate,” Mr Crepeau said….’
Full article here:
Ocean diversity and human impact: 49% decline in marine vertebrate populations between 1970 and 2012
According to an emergency edition of the WWF Living Blue Planet Report, there has been a 49% decline in marine vertebrate populations between 1970 and 2012. These estimates are based on tracking 5829 populations of 1234 species. For some fish species, the decline has been almost 75%. Overfishing, habitat destruction and climate change are held to be responsible.
Details here:
http://www.wwf.org.au/news_resources/?uNewsID=14601
Concerning the importance of marine ecosystems more generally, a concise and up-to-date list of important aspects of ocean diversity and how it has been affected by human activities is given in the UNESCO report:
Some important points from this report:
- “By the year 2100, without significant changes, more than half of the world’s marine species may stand on the brink of extinction.
- Today 60% of the world’s major marine ecosystems that underpin livelihoods have been degraded or are being used unsustainably.
- If the concentration of atmospheric CO2 continues to increase at the current rate, the ocean will become corrosive to the shells of many marine organisms by the end of this century. How or if marine organisms may adapt is not known.
- Ocean acidification may render most regions of the ocean inhospitable to coral reefs, affecting tourism, food security, shoreline protection, and biodiversity.
- Commercial overexploitation of the world’s fish stocks is so severe that it has been estimated that up to 13 percent of global fisheries have ‘collapsed.’
- There are now close to 500 dead zones covering more than 245,000 km² globally, equivalent to the surface of the United Kingdom.
- Between 1980 and 2005, 35,000 square kilometers of mangroves were removed globally.
- Between 30 and 35 percent of the global extent of critical marine habitats such as seagrasses, mangroves and coral reefs are estimated to have been destroyed.”
Causes of losses in marine biodiversity are discussed here, with some references:
Borderforce on the Streets of Melbourne. A deliberate Act to Create Fear?
The plans of the police and Australian Border Force to start patrolling the streets of central Melbourne to “randomly” check for visa details, was cancelled after very strong public protests. “The Abbott government is under pressure to explain why the police-led operation including the ABF involved stopping people for visa checks – a measure independent Tasmanian MP Andrew Wilkie compared to East Germany’s Stasi.”
Tony Windsor, the former independent Mp for New England, had the following to say:
“Mr Windsor said: “I’ve got no doubt that some of these people in Abbott’s government hope that something goes wrong domestically. That they can taunt a Muslim into doing something so that they can say that we’re the only ones that can protect you, the Labor party are too weak to protect you, vote for us,” he said, adding, “I think that’s an extraordinary agenda to go to an election on.” Full article here:
A similar interpretation of the action (diverting attention from policy failures) was also given in a detailed article by Peter Hatcher in the Sydney Morning Herald, August 29-30 (“Leadership vacuum is filled with hot air”). The Prime Minister, Tony Abbott, however, denied any knowledge of the action and blamed a poorly formulated press release for the “misunderstanding”.
Corrected sunspot history suggests climate change not due to natural solar trends
According to the International Astronomical Union (7 August 2015), sunspot activity over the last 300 years has remained more or less stable and cannot, therefore, be responsible for global warming since the industrial revolution.
“The Sunspot Number is a crucial tool used to study the solar dynamo, space weather and climate change. It has now been recalibrated and shows a consistent history of solar activity over the past few centuries. The new record has no significant long-term upward trend in solar activity since 1700, as was previously indicated. This suggests that rising global temperatures since the industrial revolution cannot be attributed to increased solar activity.”
“The Maunder Minimum, between 1645 and 1715, when sunspots were scarce and the winters harsh, strongly suggests a link between solar activity and climate change. Until now there was a general consensus that solar activity has been trending upwards over the past 300 years (since the end of the Maunder Minimum), peaking in the late 20th century — called the Modern Grand Maximum by some.”
“This trend has led some to conclude that the Sun has played a significant role in modern climate change.”
“The apparent upward trend of solar activity between the 18th century and the late 20th century has now been identified as a major calibration error in the Group Sunspot Number. Now that this error has been corrected, solar activity appears to have remained relatively stable since the 1700s.”
Full article (Science Daily) here:
http://www.sciencedaily.com/releases/2015/08/150807220750.htm
A new book on the history of climate change politics in Australia
A book on the history of climate change politics in Australia, describing the disastrous influence of the right wing media (particularly those controlled by Murdoch) and the big mining corporations has just been published. Author is Maria Taylor (“Global Warming and Climate Change. What Australia knew and buried….then framed a new reality for the public”). http://press.anu.edu.au/titles/global-warming-and-climate-change/ : A free copy can be downloaded at this address.
The book is based on Taylor’s research for a PhD at the National Centre for the Public Awareness of Science of The Australian National University. From the ANU site on her book: “Her multi-disciplinary investigation of the public record and the input of science, politics, economics, journalism and contemporary mass media has revealed for the first time how and why Australia buried a once good understanding of global warming and climate change — to arrive after 25 years at the confusion and stalemate we are still in today. “
An outline and discussion of he book is available here:
Excerpts:
“In 1989 Hawke described a “growing consensus amongst scientists” showing there was a strong chance that major climate change was on its way, that this change was linked to human activity, and this could have “major ramifications for human survival” if nothing was done.”
‘The Howard government …….. cautious climate policy positions ……. to justify it through media articles. That modelling was supported financially by the likes of the Australian Coal Association, the oil giant Exxon Mobil and the mining majors BHP and Rio Tinto.”
” ……. by 1997, many political and economic reporters were “dutifully scribing the story established by the business and political elite”.
A point to make is the role of the media in Australia, which is so dominated by the Murdoch press. That played a key role, in a sense that as the 90s rolled on it was so much easier to get out a consistent narrative if you don’t have a really diverse press. From what I saw – and what the documentary evidence showed – the ABC did have a leadership role for a long time in informing the public about climate change, but it really drew back in the late 90s. There was no other story being told.
Free-market neoliberal thinktanks, including the Institute of Public Affairs, promoted climate science denialist views and industry talking points that were picked up by the media.”
Niall Ferguson: Civilization, und Goethes Faust
Der britische Historiker Niall Ferguson, bekannt unter anderem durch sein Buch The Pity of War, in dem er die Ursachen des Ersten Weltkrieges untersucht, und weitere Bücher, hat in einem brilliant geschriebenen Buch einen Abrisss der geschichtlichen Entwicklung der westlichen Zivilisation gegeben und versucht, die Ursachen ihres Erfolges zu verstehen (Civilization. The Six Killer Apps of Western Power, 2011). Auf Seite 305 (der Penguin Ausgabe von 2012) zählt er diese killler applications auf. Sie sind: Wettbewerb, wissenschaftiche Revolution, Herrschaft des Gesetzes und der representativen Regierung, moderne Medizin, die Verbrauchergesellschaft, und die Arbeitsethik. In einer Fussnote auf Seite 324 (sozusagen als Abschluss des Buches) erwähnt er als ‘foundational texts of Western civilization’ (als grundlegende Texte der westlichen Zivilisation) die folgenden Werke: King James Bible, Isaac Newtons Principia, John Locke’s Two Treatises of Government, Adam Smith’s Moral Sentiments and Wealth of Nations, Edmund Burke’s Reflections on the Revolution in France, und Charles Darwin’s Origin of Species (und als Anhang William Shakespeare’s plays und ausgewählte Reden von Abraham Lincoln und Winston Churchill).
Diese Auswahl scheint mir etwas einseitig anglozentrisch zu sein. Wie wäre es hiermit?:
Luthers Bibel (durch Gutenbergs Erfindung des Massendruckes der direkte Anlass zur schnellen Verbreitung des Wissens und aller späteren wissenschaftlichen Fortschritte), Johannes Kepler Astronomia Nova und Harmonices Mundi, Goethe Faust I und II, Immanuel Kant Über den ewigen Frieden, Johann Sebastian Bach Matthäus Passion, Beethoven Neunte Symphonie, Alexander von Humboldt Cosmos, Gregor Mendel Vererbungsgesetze, Max Weber Die Protestantische Ethik und der Geist des Kapitalismus, Ludwig Boltzmann Entropie, Max Planck Quantum, Albert Einstein Allgemeine Relativität. Und ferner (keine ‘Grundlagen’ der westlichen Zivilisation aber vielleicht mehr zukunftsweisend als zum Beispiel Konsumerismus und Wettbewerb): Die Upaschinaden und Arthur Schopenhauer Die Welt als Wille und Vorstellung.
Auf Seiten 65-66 zählt er die wichtigsten 29 “breakthroughs” zwischen 1530 und 1789 auf. Überraschend, Keplers Gesetze der planetarischen Bewegungen fehlen, ohne Zweifel eines der wichtigsten Entdeckungen der Renaissance und von vielen als von entscheidender Bedeutung für die wissenschaftliche Revolution im 17. Jahrhundert angesehen, eine wesentliche Vorraussetzung von Newtons Gravitationslehre. Die Entwicklung des binären Systems durch Leibniz sollte ebenfalls hier stehen.
Der bekannte schweizer Ökonom H.C. Binswanger hat in einem Buch ausführlich beschrieben, wie Goethe in seinem Faust die Entwicklung der modenen Welt dargestellt hat. Faust, der Repräsentant der modernen Welt, ist ein tatkräftiger Unternehmer, sein Erfolg möglich gemacht durch die Erfindung des Papiergeldes (das die Goldwährung erstetzt), die Äquivalenz zwischen Währung und produzierten Güter, und die Eigentumsgesetze). Historisch genau beschrieben ist im Faust die folgende Sequenz: 1. Papiergeld (Bank of England), Dampfmaschine (James Watt) und damit Anfang der industriellen Revolution, Römisches Eigentumsgesetz des “Dominion”, d.h. das Recht zu benutzen und zu konsumieren: Code Napoleon). Goethe weist auch auf die potentiellen Gefahren hin: eine wirkliche Gefahr besteht darin, dass bei wirtschaftlicher Entwicklung die Konsequenzen für die Umwelt nicht in Rechnung gestellt werden. In anderen Worten, Faust ist der moderne Mann mit all seinen Stärken und Schwächen. In keinem der von Ferguson angeführten “foundation” – Texten wurde auf die potentiellen Gefahren durch die Zerstörung der Umwelt hingewiesen; Goethes Faust ist also zumindest in diesem Punkt viel zukunftsweisender.
Was die Bibel anbetrifft, nicht die King James Bibel sondern Luthers Bibel ins Deutsche übersetzt stand am Anfang der protestantischen Revolution und dem schnellen Anstieg der westlichen Macht, ihre Wirkung möglich gemacht durch Gutenbergs Erfindung des schnellen Massendruckes, von Ferguson als die wichtigste westliche Entwicklung vor der industriellen Revolution nur kurz früh in seinem Buch erwähnt. Was bei Ferguson ebenfalls fehlt ist die stärkere Betonung der typisch westlichen Musik die durch Bach, Mozart, Beethoven Wagner und viele andere zu einem Höhepunkt geführt wurde, und ein wesentliches Element des modernen westlichen Menschen ist.
Und was die Literatur anbetrifft, die von Ferguson erwähnten ‘plays’ von Shakespeare sind sicherlich schön und gross, doch welche Schlüsse auf die moderne Welt lassen sie zu? Grimmelshausen Der abenteuerliche Simplizissimus und Brecht Der Gute Mensch von Szechuan und Leben des Galilei scheinen mir in der Hinsicht relevanter zu sein.
Insgesamt, die erstaunlichen von Ferguson beschriebenen ‘Fortschritte’ (wenn man sie so nennen soll) der westlichen Welt in den letzten 300 Jahren sind vielleicht nicht mehr als ein Schluckauf in einer Geschichte, die kurz vor der Katastrophe steht, wenn wir die Fehlentwicklungen nicht in den Griff bekommen. Und können wir hoffen, dass die “foundations”, die von Ferguson gefundenen Grundlagen dieser Entwicklungen, ausreichen, eine bessere Zukunft zu sichern? Man muss wie Ferguson schon ein Bewunderer von Präsident Reagan, Margaret Thatcher und Churchill sein, um das zu glauben, und viele sind das nicht.
Ich schliesse mit einem Zitat von Noam Chomsky aus meinem vorhergehenden Post:
“Die menschliche Spezies gibt es schon vielleicht seit 100.000 Jahren und sie steht jetzt vor einem einzigartigen Moment in ihrer Geschichte. Diese Spezies ist jetzt an einem Punkt, an dem sich sehr bald entscheiden wird, in den kommenden Generationen, ob das Experiment des sogenannten intelligenten Lebens weitergehen wird oder wir fest entschlossen sind, es zu zerstören. Überwiegend erkennen Wissenschaftler, dass fossile Energieträger im Boden bleiben müssen, damit unsere Enkel eine Zukunft haben. Aber die institutionellen Strukturen unserer Gesellschaft versuchen, jeden Tropfen aus der Erde zu pressen. Die Folgen, die Auswirkungen der vorhergesagten Effekte des Klimawandels für die Menschheit in nicht sehr ferner Zukunft sind katastrophal und wir rasen auf diesen Abgrund zu.”
H. C. Binswanger. The Challenge of Faust. Science 281, 31 July 1998.
H. C. Binswanger. Money and Magic: a Critique of the Modern Economy in Light of Goethe’s Faust, University of Chicago Press 1994 (transl. from German).
http://www.nybooks.com/articles/archives/2015/oct/22/very-great-alexander-von-humboldt/
Niall Ferguson. Civilization. The Six Killer Apps of Western Power. Penguin 2012.
Noam Chomsky über den Klimawandel und die Zukunft des intelligenten Lebens auf der Erde
Noam Chomsky, der berühmte Wissenschaftler und Politik-Kommentator, in einem Interview mit dem ‘Freitag’ im MIT (Massachusetts Institute of Technology).
Auszüge:
“Noam Chomsky: Die USA sind ein Schurkenstaat, Europa ist extrem rassistisch”
“Hoffentlich gibt es endlich einen Volksaufstand gegen die vernichtende, zerstörerische Wirtschafts- und Sozialpolitik, die von den Bürokraten und den Banken kommt.”
“Die menschliche Spezies gibt es schon vielleicht seit 100.000 Jahren und sie steht jetzt vor einem einzigartigen Moment in ihrer Geschichte. Diese Spezies ist jetzt an einem Punkt, an dem sich sehr bald entscheiden wird, in den kommenden Generationen, ob das Experiment des sogenannten intelligenten Lebens weitergehen wird oder wir fest entschlossen sind, es zu zerstören. Überwiegend erkennen Wissenschaftler, dass fossile Energieträger im Boden bleiben müssen, damit unsere Enkel eine Zukunft haben. Aber die institutionellen Strukturen unserer Gesellschaft versuchen, jeden Tropfen aus der Erde zu pressen. Die Folgen, die Auswirkungen der vorhergesagten Effekte des Klimawandels für die Menschheit in nicht sehr ferner Zukunft sind katastrophal und wir rasen auf diesen Abgrund zu.”
Vollständiger Artikel hier:
Solar activity and new “little” ice age, and another interpretation
The Lomonosov State University Moscow has published a press release that presents evidence for the possibility of a small “little” ice age developing in about fifteen to twenty years. The evidence is that the sun undergoes cycles in activity indicated by the number of observed sun spots (50 per year during the previous little ice age lasting from 1645 to 1700, and 40 – 50 000 during the warmer period after it), and that we are approaching a point when activity should decrease.
“In 17th century, though, there was a prolonged reduction in solar activity called the Maunder minimum, which lasted roughly from 1645 to 1700. During this period, there were only about 50 sunspots instead of the usual 40-50 thousand sunspots. Analysis of solar radiation showed that its maxima and minima almost coincide with the maxima and minima in the number of spots.”
“If the similar reduction will be observed during the upcoming Maunder minimum this can lead to the similar cooling of the Earth atmosphere. According to Dr Helen Popova, if the existing theories about the impact of solar activity on the climate are true, then this minimum will lead to a significant cooling, similar to the one occurred during the Maunder minimum.
However, only the time will show soon enough (within the next 5-15 years) if this will happen.”
Full article here:
http://astronomynow.com/2015/07/17/diminishing-solar-activity-may-bring-new-ice-age-by-2030/
I have asked Professor Michael Box, a renowned climate physicist from the University of NSW, Sydney, to comment on this post and he has given me permission to add his comments here.
Klaus,
Yes, it is causing quite a stir, isn’t it? Let me see how much light I can shed.
The analysis techniques used to underpin the prediction of very low sunspot numbers (principal component analysis) is well known and ‘valid’ as to what it does. Using it to project into the future is somewhat less valid, as other factors which have not shown up in the past data may be waiting in the wings. I guess I would rate the chances of very low sunspot numbers in the 2030s as less than 50-50, but certainly not at, or close to, zero.
So that brings us to the more important issue of the impacts. The Little Ice Age (so-called) is certainly ‘real’, although many questions remain.
When did it begin? I’ve seen dates of anywhere from 1300 to 1450 – both well before the start of the Maunder Minimum in 1645.
When did it end? Again I’ve seen dates as late as 1850 (well after the end of the MM in 1715), which might well imply that the only reason it did end is the onset of global warming!
Was it global, or regional? There is plenty of evidence from Europe and some from North America. I’ve seen a suggestion of some evidence from New Zealand. However there do seem to be many questions around the uniformity of the cooling.
So that brings us to the really key question of the causes/drivers. Solar activity is certainly one possibility, although as I’ve indicated the MM certainly couldn’t have started it. It may have made things just a little bit cooler – say 0.2 C – but it wasn’t the cause! Other suggestions have been a slowing of the Gulf Stream (it has slowed significantly in the past. ~11,000 years ago); volcanic activity (a couple of major eruptions followed by some feedbacks); and ‘orbital forcing’. We know that changes in the Earth’s orbit are the drivers of the glacial-interglacial cycle (something one of the authors of the paper in question is clearly ignorant of!), and these drivers don’t stop and start, but are on-going. We probably are heading ever so slowly for the next glacial.
Like most scientists who have made ‘meaningful’ comments, my view is that, if it does happen, it will reduce global warming by ~0.1 C – or delay it by ~10 years. And that delay would only be temporary, and temperature would zoom ahead in the years that followed.
Interesting to compare this critical account with a story published in news.com.au (a Murdoch site), in which the ‘coming ice’ age is more or less presented as a fact (“Earth heading for ‘mini ice age’ within 15 years’) and rounded up with drawing attention to the present cold front affecting SE Australia:
“Tropical-style thunderstorms, accompanied by heavy snowfalls, roared through the Blue Mountains, west of Sydney, and towns as far as Orange on Saturday night.”
Full story here:
Marching into the Past: Cutting down on Renewable Energies and the Freedom of the Press
From the Sun Herald ( a Fairfax weekend newspaper) 12.July 2015:
“Tony Abbott has been warned he is putting international investment at risk after ordering the $10 billion Clean Energy Finance Corporation not to finance new wind power projects.”
Both the Prime Minister and the Treasurer have repeatedly claimed that wind farms are noisy and ugly. No such comments about a new open cut coal mine in fertile agricultural lands in NSW, just approved by the Federal government.
According to the ABC on 13.7.15, “small scale solar power” projects are also banned.
“Prime Minister Tony Abbott has been accused of unprecedented political interference in the ABC by demanding the broadcaster move panel program Q&A into its news division before he lifts a boycott of the program.
In a letter sent to ABC chairman Jim Spigelman on Friday, Mr Abbott said he would be happy to lift a ban on his frontbenchers appearing on Q&A if the ABC transferred the program from its television department to news and current affairs.”
Urgent action necessary: Contrasting futures for ocean and society from different anthropogenic CO2 emissions scenarios
Professor Ove Hoegh-Guldberg, Director of the Global Change Institute and Professor of Marine Science at The University of Queensland, Brisbane, Deputy Director of James Cook University’s Centre for Excellence in Coral Reef Studies, and an ARC Laureate Fellow in 2013, is one of the authors of a paper just published in Science vol. 349, 3 July 2015, no. 6243, DOI: 10.1126/science.aac4722: http://www.sciencemag.org/content/349/6243/aac4722. in which the effects of climate change on the oceans are discussed under two scenarios, one if we continue as now, the other if we reduce temperature rise to 2 degrees.
Professor Hoegh-Guldberg has also published an article in Conversation accessible to the wider public, in which he emphasises the need for urgent action if we want to avoid disaster: “……..the ocean system could not be more important: it regulates the global temperature and atmosphere, feeds 3 billion people, and largely determines our weather. The ocean also has lots of “inertia” – which means that getting the ocean to change takes a lot of energy, but once it begins to change, slowing it down becomes more or less impossible…..” . Full article here:
4th book review of Klaus Rohde ed.: The Balance of Nature and Human Impact. Cambridge University Press 2013
The fourth review of the book edited by me has just been published in Quarterly Review of Biology, University of Chicago Press 90, pp. 211-212, June 2015. Reviewer is Professor Andrew Goudie, Professor of Geography, Oxford University, well known for his work on desert geomorphology, dust storms, weathering, and climatic change in the tropics, and his books on human impacts on the environment. For copyright reasons I include only two excerpts:
“There is more than ample evidence that humans are having an increasing impact on the environment through changes in land use and land cover, climate change, and globalization of organisms. A big question, which this book aims to answer is ‘what will be the ecological responses to such changes’? Will certain tipping points be passed for certain organisms and ecosystems?
The book is composed of 27 chapters and has 30 authors from a range of countries, with a particularly strong contingent from Australia. It covers various taxonomic groups, including plants, nematodes, mammals and birds, and a range of marine, freshwater and terrestrial environments. It is very strong with respect to debates about equilibrium and non-equilibrium states at a variety of scales from populations to communities and to ecosystems of varying spatial extent. ”
“………… individual chapters have great merit and the overall message is a very important one. Parts I, II and III are valuable because of the light they throw on equilibrium concepts, while Part V includes useful case studies…….”
Earlier reviews here:
https://blog.une.edu.au/klausrohde/2013/11/10/review-of-klaus-rohde-ed-the-balance-of-nature-and-human-impact-cambridge-university-press-2013/
https://blog.une.edu.au/klausrohde/2013/12/17/2nd-book-review-of-klaus-rohde-ed-the-balance-of-nature-and-human-impact-cambridge-university-press-2013/
”
The President of the Australian Human Rights Commission on Changes to the Citizenship Laws
The President of the Australian Human Rights Commission, Professor Gillian Triggs, according to the Sydney Morning Herald 6-7 June, 2015, “has warned that Australian democracy is under threat” by “government moves to expand discretionary powers that may be exercised with limited or no judicial scrutiny”.…… “The overreach of executive power is clear in the yet to be defined proposal that those accused of being jihadists….will be stripped of their citizenship if they are potential dual nationals”.
The Immigration Minister, Peter Dutton, had earlier attacked Professor Triggs “for making outrageous and offensive claims that were a ” ‘complete disgrace’ “. Similarly, he attacked Greens Senator Sarah Hanson-Young who had visited the detention centre on Nauru and had complained of being spied upon during her visit.
Also from the Sydney Morning Herald 6-7 June: Nepalese parents with her 5 year old baby were forced to return to the detention centre on Nauru to live in large tents, where children as young as two had been assaulted, according to a former child protection worker for Save the Children Victoria Vibhakar.
In this article (The Guardian), attention is drawn to warnings by Professor Triggs about repeated moves not only by the federal parliament and government, but by those in various states, to introduce ” ‘scores of laws’ threatening fundamental freedoms”.
A snapshot of Australian politics 5th June 2015: Jail for reporting abuse in detention centres, free ride in climate change, loss of citizenship without recourse to law, no ethics lessons in schools, no tax disclosure for billionaires!
Some quotes from the Sydney Morning Herald 5th June 2015, which provide an interesting insight into the political situation in Australia run by the right-wing Liberal/National government under Prime Minister Tony Abbott.
1) Australia has chosen an extreme hardline policy on refugees arriving by boat from various Southeast and South Asian countries, mainly Indonesia, turning boats back and imprisoning those refugees who made it to Australia in detention centres on Manaus Island, Papua New Guinea, and the “independent” Pacific Island nation of Nauru. It has now introduced a law that would make it a criminal offense to report abuse in these centres (reports of such abuse including sexual crimes had made it into the press in the past):
“Doctors and teachers working in immigration detention facilities could face up to two years in prison if they speak out against conditions in the centres or provide information to journalists, under sweeping new laws to gag whistleblowers.
The Border Force Act, which was passed quietly on May 14 by both major parties, clamps down on “entrusted people” in detention centres recording or disclosing information about conditions in centres such as those on Nauru and Manus Island.
Under the heading of “secrecy and disclosure provisions”, the act says releasing information is only permitted by the secretary of the department responsible for detention centres.”
“In a media release last month, Immigration Minister Peter Dutton said the new law would “further strengthen the government’s ability to protect Australia’s border.”
According to Dr. Richard Kidd, one of the founders of the Doctors for Refugees, “the new law was taking away all transparency and accountability”, and “it is absolutely clear that doctors and nurses are expected as part of their registration to put the best interests of their patients first and that includes advocating for [people] being denied appropriate health services or being abuse in some way” .
2) Soon after taking over government, Tony Abbott abolished the carbon tax, reduced the renewable energy target, tried hard but ultimately failed to exclude discussion of climate change politics at the G20 meeting in Brisbane, etc.
“Australia has become a climate change “free-rider”, dropping off the list of nations taking “credible” action to curb greenhouse gas emissions, according to a panel led by former UN Secretary General Kofi Annan.”
3) The government wants to introduce a law (supported by the Labor party) to deprive “terrorists” with (potential) dual citizenship of their Australian citizenship without recourse to the law. Potential dual citizens include those who do not actually possess but qualify to obtain a second one.
“Potentially hundreds of Australians could be stripped of their citizenship and then deported, without recourse to the courts as to the merits of their defence, once the Australian Parliament passes tough new counter-terrorism laws with the support of the opposition.”
4) The Liberal/National government in the largest Australian state, NSW, is attempting to weaken access to non-religious ethics classes for those who do not wish to take religion lessons, an option introduced by the previous Labor government:
5) The previous Labor government had introduced a law which obliged rich companies to disclose their income. The present Liberal/National government, in draft laws just released, made 700 private (but not public) companies exempt from that disclosure, because public knowledge might expose them to potential losses in commercial negotiations.
“James Packer’s Consolidated Press Holdings is among about 700 private companies that are excluded from having their tax details published by the Tax Office under draft laws released by the Abbott government.”
“Public companies with more than $100 million turnover will still be required to report taxable income, total income and tax paid. “
“Shadow assistant treasurer Andrew Leigh said Labor’s rules would have allowed for an “open and informed public discussion” about how much tax Australia’s biggest companies pay.”
Karl Kraus: The Last Days of Mankind. God created Man not as a Consumer but as a Human Being
We are living in a world in which conflicts, be they economic, military, cultural or religious, are getting worse with little inclination of the various “players” to compromise and find a solution acceptable to all. Each side believes or pretends to believe that it has the right on its side, or, in other words, that it has reached the pinnacle of history. In this, the world situation closely resembles that just before the first world war. If we want solutions, it may be helpful to look at how the world situation 100 years ago was reflected in intelligent/perceptive minds. One such mind was Karl Kraus, the famous Viennese satirist and critic who died in 1936. The “grumbler” or “begrudger” (original German “der Nörgler”, a character based on himself), in his satirical antiwar play “The last days of mankind” (Die letzten Tage der Menscheit, 200 loosely connected scenes largely based on actual events and characters, written during and in the first years after the first world war) says, according to http://www.thebaffler.com/salvos/hail-grumbler
“God created man not as a consumer or producer but rather as a human being. That the means of life should not be the goal of life. That the stomach should not outgrow the head. That life is not exclusively based on the profit motive. That a human being is allotted time in order to have time and not to arrive somewhere faster with his legs than with his heart.“
And, according to: http://thelastdaysofmankind.com/, referring to Kraus’s readings of portions of the play,
organized group travels to the battelfields of the war and the graves of the dead are a disgrace:
“The dead in their millions are hardly cold in the ground. What Kraus reads invokes the sacrifices made in passing, barely, cynically, tritely, before the details of itineraries, highlights, hotels, travel arrangements, their great advantages and pleasures of first class seats and tickets, etc., are expounded with an extraordinary gusto. This is some holiday! It is as grotesque and shameful as Kraus’s reading makes it.”
The play terminates in an apokalyptic scene, the extinction of mankind. Mankind in its entirety is the “antihero”, unworthy of life on earth because it has permitted the cruelties of war.
Kraus had written earlier in the play: “Lord forgive them for they do know what they do.”
Not to forget, Kraus wrote for German/Austrian readers and audiences. I am not aware of any English writers, excepting perhaps Thomas Hardy on a much milder note, who attacked their leaders and compatriots with a similar degree of causticity.
Karl Kraus has been largely neglected in the anglophone countries, but translations of some of his works are now becoming more frequent. And considering the situation in the world today, his insights are of considerable importance. Indeed, it seems that little has changed over the last 100 years. The political situation worldwide is now as unstable as it was before the first world war when Karl Kraus wrote his play (conflicts between Russia and the EU over the Ukraine, between China and the USA over Southeast Asian islands; almost total collapse of social structures in Libya/Syria/Iraq/Afghanistan/some African countries largely as the result of wars; overpopulation pressure in Bangladesh and many other countries in Africa and elsewhere leading to mass migrations of refugees into more affluent countries). And: the economic outlook of the populace and its rulers in the so-called “Western”countries is similar: consume! consume! steered into this fallacy by much of the media which are largely under the thumb of the rich “elite”. Elections are won or lost not because of the merits of a policy concerning the future of the nation and indeed of mankind, but because of promises of short-term profits. – The results of the first world war were disastrous, directly leading to the vastly more devastating events of the second world war. However, what is happening now may be even worse: the survival of mankind is under threat if the effects of overpopulation, overconsumption and enviromental destruction, particularly that caused by climate change, are not brought under control.
Abridged English translation: The last days of mankind; a tragedy in five acts. an abridgement translated by Alexander Gode and Sue Allen Wright. New York: F. Ungar Pub. Co. 1974. ISBN 9780804424844.
In the preface to the book edition Karl Kraus wrote ” Die Aufführung des Dramas, dessen Umfang nach irdischem Zeitmaß etwa zehn Abende umfassen würde, ist einem Marstheater zugedacht. Theatergänger dieser Welt vermöchten ihm nicht standzuhalten.” (The performance of the play, which would comprise about ten evenings, is meant for a Mars theatre. People of this world would not be able to take it).
Free Markets and Free Trade, Ecology and Economics
(This article was first published as a Google knol and then transferred to wordpress.com. I re-publish it here as a basis for discussion. © Klaus Rohde).
Free Markets and Free Trade, Ecology and Economics
The Theoretical Foundations of Free Market Economy and Ecology
Abstract
Darwin’s theory of evolution by natural selection was deeply influenced by a leading geologist, a demographer and an economist, who had the ideas that geological changes in the past can be explained by the same factors that are operative now, that changes have been gradual, that demand grows faster than supply, leading to competition for resources, and that market forces lead to equilibria. Darwin’s theory is at the basis of much of modern ecology, i.e., equilibrium ecology. Its three pillars are competition for resources (struggle for existence), survival of the fittest, and equilibrium in nature. – In parallel, the pillars of free market economy are competition for resources, the principle of comparative advantage, and equilibria. – Here we examine how recent findings on ecology have changed our views on equilibrium in ecological systems, and whether these findings can be applied to economics.
Introduction
Darwin’s theory of evolution by natural selection was deeply influenced by a leading geologist of his time, Charles Lyell [1], by a leading demographer, Thomas Robert Malthus [2], and by a leading economist, Adam Smith [3]. Lyell proposed the theory of uniformitarianism, according to which geological patterns over time were shaped by the same factors that are effective today, and that changes occurred gradually. Malthus realized that demand grows faster than supply, leading to competition for resources, and Smith proposed that market forces regulate prices establishing an equilibrium, thus avoiding the catastrophe predicted by Malthus. He also proposed a mechanism justifying free trade between countries, i.e., the idea of absolute advantage, soon to be replaced by Ricardo’s principle of comparative advantage [4]. – Darwin’s theory [5] is at the basis of much of modern ecology, i.e., of what is best called equilibrium ecology [6]. Its three pillars are competition for resources (or struggle for existence), survival of the fittest, and equilibrium in nature. – In parallel, free market economy is largely based on Smith’s and Ricardo’s ideas. Its pillars are competition for resources, the principle of comparative advantage, and equilibrium in economy, although much has happened in the last 200 years and some economists, at least, have incorporated non-equilibrium, ecological and psychological approaches.- Here we examine how recent findings on ecology have changed our views on equilibrium in ecological systems, and whether these findings can be applied to economics.
Definitions
First, I give definitions of the terms used.
Absolute advantage:
a country has an absolute advantage over another country in producing something, if its production costs for this product are lower.
Autecology:
the study of the ecology of particular species and populations.
Character displacement:
a change in the characteristics of a species due to competition with other species, or due to reinforcement of reproductive barriers.
Comparative advantage:
a country has a comparative advantage over another country in producing something, if its “relative production costs” are lower (or: for which the “opportunity cost” of production is lower: see opportunity cost).
Competition:
process which leads to the survival of the fittest within species (intraspecific competition) or between species (interspecific competition).
Density dependence:
dependence on population density (individuals per unit area).
Equilibrium:
balance in economy and nature.
Evolution:
the changes in the kinds of species and their characteristics over time.
Limiting resource:
a resource (food, space, etc.) which is potentially in limited supply, i.e., which limits the size of a population even if other resources are abundant.
Malthusian catastrophe:
catastrophe arising from the discrepancy in the increase of demand and supply.
Natural selection:
mechanism which drives evolution by the survival of the fittest.
Niche:
a species’ place in nature, or: a species’ place in multidimensional hyperspace (niche space with many niche dimensions; see: niche dimension).
Niche dimension:
any of the many dimensions (such as habitat, food, salinity, environmental temperature, etc.etc.) of a niche defining a species’ place in nature.
Non-equilibrium:
non-balance in nature.
Opportunity cost:
amount of product which must be given up in order to produce one more unit of another product.
Optimization:
optimal adaptation to environmental conditions.
Reinforcement of reproductive barriers (= Wallace effect):
change in characteristics of a species which prevents hybridization with a closely related (congeneric) species, due to its co-occurrence with such species.
Uniformitarianism:
the theory according to which geological patterns over time were shaped by the same factors that are effective today, and that changes occurred gradually.
Vacant niche:
the potential that more species can exist in a habitat than are present at a particular point in time.
Vagility:
the degree with which individuals or species can move around in and between habitats.
Wallace effect:
see reinforcement of reproductive barriers.
The benefits of free trade
There can be no doubt that free markets/free trade have been of great benefit to many countries, lifting millions out of impoverishment. The aim of this article is not to put this in doubt, but to warn against raising free market economics to a dogma that has to be followed under any circumstances, disregarding local conditions and potential dangers to developing (and developed) countries.
History of concepts
As pointed out above, much has happened in economics theory in the two centuries since Smith and Ricardo. This article does not attempt to consider all such developments, but restricts itself to looking at some important “classical” assumptions, which are still dominant in the field.
Free markets in economy
Ricardo’s principle of comparative advantage was developed as a justification for free trade, replacing the earlier justification based on absolute advantage by Adam Smith. It means that even if a country has an absolute advantage over another in producing something, it may still be advantageous to concentrate on another product, for which it does not only have an absolute advantage, but a comparative advantage as well, i.e., for which its “relative production costs” are lower (or: for which the “opportunity cost” of production is lower, where opportunity cost is defined as the amount of product which must be given up in order to produce one more unit of the other product). Even from the viewpoint of the country which has an absolute disadvantage in producing any product, concentration on products with the lowest opportunity costs will be of benefit to it. In other words, both countries will benefit by concentrating on products which they can produce comparatively more cheaply: the overall outcome will be that the total product of both countries will increase. Suranovic (2007) lists a number of assumptions on which the principle is based [7]. They are (for the simplest version of the model): 1) labour is homogeneous within but heterogeneous between countries; 2) goods can be transported without cost between countries; 3) labour can be re-allocated without costs between industries within but not between countries; 4) there is no unemployment; 5) there are differences in production technology across industries and countries; 6) labour and goods markets are perfectly competitive in all countries; 7) firms maximize profit and consumers maximize utility.Obviously, most of these assumptions are unrealistic in many cases of the modern world (and probably always were). However, they are accommodated in more complex models developed to “rescue” the principle. Another possible objection is that the principle, which seems to make perfect sense if the simple case of two countries is considered, may not apply to the far more complex case of many countries: does complexity perhaps lead to quite different dynamics? In ecology, the degree of complexity of an ecosystem may affect its stability: an important problem is whether complexity makes an ecosystem more or less stable. The question therefore arises: how common are conditions which legitimize application of Ricardo’s principle? Important here is evidence provided by Chang that free trade, in history, has always been used by more advanced countries to keep less advanced ones down, preventing them from developing their own industries [8]. – One particularly pernicious example of the misuse of free trade is the opium wars between Britain and China 1839 to 1842 and 1856 to 1860, not long after Ricardo’s principle was developed. They led to corruption in India (where opium was grown) and in China (which was forced to import it), all in the name of free trade: Britain needed the opium trade to pay for its valuable imports from China. This suggests the possibility that the principle may well work for countries which are not too dissimilar (in size, technology, education, tradition, etc.), but that it may be inapplicable to countries that differ vastly in their competitive abilities, opening the way to the innate viciousness of man that tempts the stronger “partner” to misuse its power (see for instance the collapse of the latest (last?) Doha round of free trade negotiations). – More generally, the principle (or model, like most models) abstracts from the psychological deficiencies of the players in the field, making false assumptions and therefore leading to wrong predictions.Equilibrium or not in ecology?
What can ecology teach us in this regard?
At the basis of modern evolutionary theory and ecology is Darwin’s theory of natural selection. Darwin was influenced by the ideas of Thomas Malthus and Adam Smith. According to Malthus, demand grows faster than supply, because populations increase exponentially and food supply arithmetically, leading to a “struggle for existence” and “survival of the fittest”. According to Adam Smith, free markets are regulatory mechanisms acting on the basis of supply and demand, leading to self-adjustment of prices (the “invisible hand”), i.e. to an equilibrium. The disaster predicted by Malthus (the “Malthusian catastrophe”) is avoided by competition (selection). In other words: equilibrium assumptions are an essential ingredient of the theory of natural selection. Darwin wrote in his Origin of Species that “battle within battle” must be continually recurring with varying degrees of success, but in the long-run forces are nicely balanced. One of the great modern ecologists, Hutchinson (1948 [9]), took it for granted that stability (owing to “self-correcting mechanisms”) is characteristic of most ecological systems and permits their persistence. According to the great evolutionary biologist Dobshansky (1957 [10]), natural selection and with it the evolutionary process result from competition, and “therefore are governed by density-dependent factors”. To this day, the belief of the overriding importance of competition between individuals and species in ecological systems, resulting in equilibrium conditions, is widespread. However, is this belief really justified? Important ecologists have pointed out repeatedly that equilibrium conditions in nature are not as common as usually assumed. Thus, Andrewartha and Birch (1954 [11]) did not recognize the predominant role of competition and the general existence of equilibria. More generally, they objected to the approach explaining differences between species by competition for limiting resources resulting in character displacement, pointing out that one should expect to find similar species in similar habitats. One should rather ask: why can species with different ecological requirements live together? – Hengeveld and Walter (1999) distinguished two mutually exclusive paradigms in ecology, the demographic and autecological one [12]. In the former, ecological systems are supposed to be driven by optimization processes (i.e., by processes that lead to a rather fast adaptation to a supposedly more or less constant environment, by competition of individuals and species) leading to equilibrium. In the latter, emphasis is on idiosyncratic adaptations and reproduction of populations and species. According to Hengeveld and Walter, the former paradigm is unrealistic, because environmental conditions change all the time, not permitting short-term optimization. – Rohde (2005) http://www.cambridge.org/9780521674553 [6]), based on a survey of much evidence from various sources from the plant and animal kingdoms, concluded that non-equilibrium is more common than equilibrium in nature. His distinction of non-equilibrium and equilibrium ecology corresponds to a large degree with the two paradigms of Hengeveld and Walter, although he does not consider them to be mutually exclusive. Rather, equilibrium is more likely in communities consisting of vagile and/or large individuals and/or large populations. Literature indicates that equilibrium systems, in which interspecific competition is common, are the exception rather than the rule. – Important here is the demonstration that niche space is largely empty, i.e., many potential niches have never been filled. In other words, there is an abundance of vacant niches. For example, evidence clearly shows that diversity of animals has continually increased over hundreds of millions of years to the present, and that similar habitats often contain vastly different numbers of species.
What can ecology teach us about economics?
As we have seen, the fundamental assumptions of classical economics and equilibrium ecology are surprisingly similar. The pillars of the former are competition for resources, the principle of comparative advantage, and equilibrium; the pillars of the latter are competition for resources (struggle for existence), survival of the fittest, and equilibrium. Concerning ecology, we have seen that resources are seldom exhausted, that competition occurs but is not of the overriding importance often assumed, and that equilibrium conditions are not as common as non-equilibrium ones. This should give us some reasons to at least have a closer look at the assumptions of free market economics. There can be little doubt that there often is competition for resources, but it seems that shortages frequently are of a temporary nature. On the supply side: recent evaluations suggest that wave energy alone would be sufficient to provide all of Australia’s energy; solar energy in Saharan Africa, among others, is only being talked about. On the demand side: demand is artificially and almost(?) hysterically driven up by advertising that plays on greed and “doing better than your neighbour”; and is the political hysteria leading to an ever increasing expenditure on defense perhaps the result of aggressive instincts of man cleverly exploited by nations’ military-PR industrial complexes? – Equilibrium in economy appears to be a fairly transient condition, as shown at this very moment by the global financial crisis.
Conclusions
So, data suggest that some of the basic assumptions both of equilibrium ecology and free market economics are flawed. However, it must be emphasized that in ecology competition and equilibrium are common under certain conditions, and that in economy free trade may well be of benefit when certain conditions are met. In ecology, an autecological approach, which involves a careful and often long-term study of populations and species, may often be of greater use than a demographic one, and in economy, a careful analysis of local conditions permitting a decision on the benefits of free trade may often be useful, in particular when a powerful nation deals with a small developing one.
Addendum
Since this knol was published, Paul Krugman was awarded the Nobel Prize for Economics for work which clearly implies that Ricardo’s principle does not realistically describe what is actually happening.
References
Lyell, Charles (1830). Principles of Geology. John Murray, London.
Malthus, Thomas R. (1798). An Essay on the Principle of Population. J.Johnson, London.
Smith, Adam (1776). An Inquiry into the Wealth of Nations. Thomas Nelson, Edinburgh.
Ricardo, David (1817). On the Principles of Political Economy and Taxation. John Murray, London.
Darwin, Charles (1859). On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life. John Murray, London.
Rohde, K. (2005). Nonequilibrium Ecology. Cambridge University Press, Cambridge.
Suranovic, S.M. (2007). International Trade Theory and Policy. The Theory of Comparative Advantage – Overview. http://internationalecon.com/Trade/Tch40/T40-0.php
Chang, Ha-Joon (2002). Kicking away the Ladder: Policies and Institutions for Economic Development in Historical Perspective. Anthem Press, London.
Hutchinson, G.E. (1948). Circular causal systems in ecology. Annals of the New York Academy of Sciences 50, 221-246.
Dobshansky, T. (1957). Discussion, from Andrewartha, H.G.: the use of conceptual models in population ecology. Cold Spring Harbour Symposia on Quantitative Biology, p.235.
Andrewartha, H.G. and Birch, L.C. (1954). The distribution and abundance of animals. University of Chicago Press, Chicago.
Hengeveld, R. and Walter, G.H. (1999). The two coexisting ecological paradigms. Acta Biotheoretica 47, 141-170.
Acknowledgement
I wish to thank Peter Rohde for some helpful comments.
9 Comments
![]()
Booms and busts in the global economy. Fuzzy Chaos Modelling in Ecology and Economics
Background
Chaos theory applied to ecology has shown that chaotic fluctuations in population sizes occur when a population exceeds a certain rate of intrinsic population growth. In nature, populations (metapopulations) are often composed of several to many subpopulations, which are largely (not necessarily completely) segregated from each other. Fuzzy chaos modelling, which considers the dynamics of a metapopulation comprised of many subpopulations, shows that the amplitude of chaotic oscillations is reduced in the metapopulation, even though each subpopulation retains the “normal” degree of chaos. Generally, the greater the number of subpopulations, the smaller the oscillations in the metapopulation. Here we examine whether these findings can be applied to economics. Is a single completely globalized economy perhaps more liable to undergo violent market upheavals than a world economy in which national economies have retained some degree of independence?Chaos theory in biologyMay (e.g. 1975 [1]) and others after him, using the apparently simple nonlinear equation for population growth xt+1= rxt (1- xt) (where xt= size of population of generation t, xt+1= size of population of generation t+1, r = intrinsic rate of population growth), have shown that chaotic fluctuations in the size of populations arise due to high intrinsic (not affected by environmental influences) rates of population growth r. When population growth is low, populations are at equilibrium, reaching a steady-state with a single value of population size. When reproductive rates exceed 3, there are at first 2 quasi-equilibrium values, followed (with increasing reproductive rates) by 4, 8 and 16 quasi-equilibrium points. At rates exceeding r=3.57, population sizes fluctuate chaotically (Figures 1 and 2). These fluctuations seem to be random, but are in fact strictly deterministic. The fluctuations are highly sensitive to initial conditions, i.e. small differences in the initial population size lead to very large differences in future fluctuations, which makes predictions about the future impossible.

Figure 1: Bifurcation diagram for a single population, showing population sizes x (as the proportion of the crowding level 1) plotted against reproductive rates r. Insets show changes of population sizes of populations with selected reproductive rates plotted against time. Note: the population size is at a stable equilibrium with single values of x until a certain value of r (larger than 3) is reached. Beyond this, populations first alternate between two quasi-equilibrium points, then between 4, 8 and 16. At r=3.57 fluctuations in population size become chaotic. Note: x never exceeds the crowding level 1.

Figure 2. As Figure 1, but shown only for r-values above 3.50.
Fuzzy chaos in ecology
Rohde and Rohde (2001 [2]), using fuzzy chaos modelling, which sums all values of subpopulation sizes at each particular reproductive rate, have shown that chaotic fluctuations are reduced in metapopulations consisting of several largely independent subpopulations with different reproductive rates, although each single subpopulation still undergoes chaotic fluctuations.
Reduction generally increases with increasing numbers of subpopulations. It decreases when subpopulations are selectively weighted, because a few large subpopulations outweigh a large number of smaller ones. The fact that chaos is reduced in the metapopulation is the effect of how chaos is measured: in the metapopulation, individual values are added and chaos in the resulting net population is necessarily suppressed, in spite of the fact that each subpopulation retains the chaos pattern of a single population. The resulting compression of the chaotic band in the metapopulation is entirely a consequence of the fact that fluctuations in the size of subpopulations are out of phase with each other. An example is given in Figure 3, which shows a bifurcation diagram for a metapopulation consisting of 5000 subpopulations (illustrated only for reproductive rates of r=3.50 and larger). Note that the width (amplitude) of the fluctuations, compared with Figures 1 and 2, is significantly reduced except for a few r-values.

Figure 3. Bifurcation diagram for a metapopulation consisting of 5000 subpopulations shown only for r-values above 3.50. Note: chaotic fluctuations above r=3.57 are still apparent, but much compressed. Strong fluctuations are largely restricted to a few values of r (3.63, 3.74, 3.84).
Application of fuzzy chaos modelling to economics
Can these findings be applied to economics? They certainly suggest that chaotic fluctuations, because they are all in phase (i.e., all troughs occur together, as do the peaks), are much stronger in single large economies or in one completely globalized economy, than in the world economy consisting of national economies that are, to a degree, separated. Because “peaks” and “troughs” of the fluctuations of individual economies are out of phase in the latter case, resources – on a world-wide basis – during a recession (bust) would not be devastated to the same degree as they would be in a single global economy, at least not at the same particular point in time. In a nutshell: imagine a world economy which is completely globalized, without any economic boundaries, and imagine a world-wide economic collapse caused by excessive debts (or some other factors) at the centre of that economy, for example the United States. The social consequences may be disastrous, in particular for poorer countries, much more so than in a situation where national economies would have retained some degree of independence and are therefore less affected by a simultaneous collapse. Naturally, booms in a fragmented world economy also would be reduced relative to those in a single globalized economy.Of course, one can only speculate how such segregation could be maintained. Would the existence of different financial systems in the world (such as the traditional Western capitalist system and the Islamic finance system) perhaps be useful? After all, during the Asian financial crisis in the 1990’s Malaysia escaped the worst consequences of the collapse because it sought refuge in Islamic financing, thus isolating itself from the Western banking system and particular the IMF. Reasons inherent in the philosophy behind Islamic financing may be partly responsible, but in our context it is important that two different systems existed which were responsible for a “decoupling” of the economies.- On a smaller scale: would the breaking up of the few oversized financial institutions (banks) into smaller units, as recently suggested by Paul Volcker, the former Chairman of the Federal Reserve, perhaps help in avoiding future large-scale collapses ? Serious errors committed by managers of one bank would not affect other banks, at least if the break-up would go hand in hand with the introduction of regulations that ensures a certain degree of segregation in the banks’ practices. After all, larger is not always better. Perhaps it is time to have another look at Schumacher’s (1973) classic: Small is Beautiful: Economics As If People Mattered [3]. Possible objectionsIt is important to note that in the fuzzy chaos model, individual subpopulations (or national economies) still exhibit the usual degree of chaos, even though the metapopulation (or world economy) shows reduced chaos. This raises the question as to whether the chaos exhibited by the net world economy is a valid metric to use. One could argue that what matters to the individual in the world economy is not how chaotic the sum of all economies is, but how much chaos they are subjected to. – An objection to this objection is: it all depends on the mechanisms available for transferring funds (“help”) from one economy to another. In a single globalized economy all individual economies would be in a bust (and boom) at the same point of time, and transfer between economies in a bust would be severely limited. In economies at different stages of the cycle, transfer should at least in principle be possible, if appropriate mechanisms were developed. – This corresponds to what we find in nature. In species of animals and plants threatened by extinction, those consisting of metapopulations with many subpopulations have a greater chance of survival than species with a single population. In times of severe crisis, some subpopulations of the former will disappear, but their habitats can be resettled by a few individuals from other habitats, because subpopulations are nevercompletelyisolated from each other. In the latter, once the population is gone, it cannot recover. Another possible objection is that all this is an exercise in theory, but that it will be impossible to change the world’s economic system in such a way that effective interactions between economies will be, to a degree, prevented. However, there may be cultural and environmental reasons in addition to economic ones, which may make it desirable to maintain a certain degree of separation between national identities, enhancing our motivation for introducing appropriate measures. At this stage we do not know how a total globalization would affect cultural diversity and the environment, both essential for humanity’s survival. South Korea’s plan to lease 1 1/2 million hectares of land in Madagascar for growing corn to be exported to South Korea, may be an indication of things to come. Madagaskar has one of the most diverse ecosystems on Earth and the consequences of such huge monocultures would be disastrous. Other examples, already existent now, are the vast palmoil plantations in Borneo and the huge cattle ranches in the Amazon. Borneo and the Amazon have the Earth’s richest and second richest tropical rainforests, respectively.
Conclusion
I realize that this approach is highly unconventional and may not be applicable to economics. Nevertheless, it may induce people to think the problem over, perhaps initiating a discussion on this site.
References
May, R.M. 1975. Deterministic models with chaotic dynamics. Nature 261, 903-910.
Rohde, K. and Rohde, P.P. 2001. Fuzzy chaos: reduced chaos in the combined dynamics of several independently chaotic populations. American Naturalist 158, 553-556.
Schumacher, E. F. 1973. Small Is Beautiful: Economics As If People Mattered. Harper & Row. N.Y.
Acknowledgement. I thank Peter Rohde for many very helpful comments. Peter was involved in developing the fuzzy chaos model and wrote all the programs for it. © Klaus Rohde
4 Comments
The Chief Business Adviser to the Prime Minister on Climate Change, and Continuing Rise in Global Carbon Dioxide Levels
According to the Sydney Morning Herald 9.5.2015, ”
“Climate change is a hoax led by the United Nations so that it can end democracy and impose authoritarian rule, according to Prime Minister Tony Abbott’s chief business adviser.
Maurice Newman, the chairman of the Prime Minister’s business advisory council, has written in The Australian that scientific modelling showing the link between humans and climate change is wrong and the real agenda is a world takeover for the UN.
This is not about facts or logic. It’s about a new world order under the control of the UN “
Full article here:
Perhaps Maurice Newman can explain the following:
The Global Monitoring Division of NOAA/Earth System Research Laboratory has published data which show that for the first time since measurements began, the global monthly mean carbon dioxide level has exceeded 400 parts per million in March 2015, a rise of more than 120 parts per million during the industrial age.
(Graph from Ed Dlugokencky and Pieter Tans, NOAA/ESRL (www.esrl.noaa.gov/gmd/ccgg/trends/)
For methods, interpretation and links to other relevant sites see:
http://www.esrl.noaa.gov/gmd/ccgg/trends/global.html
Deutscher Widerstand gegen Hitler/ German Resistance against Hitler
In diesem zweisprachigem Knol werden einige wichtige Beispiele des Widerstandes gegen Hitler besprochen.
In this bilingual knol some important examples of resistance against Hitler are discussed.
Georg Elser, Dietrich Bonhoeffer, Kardinal von Galen, Claus von Stauffenberg, Edelweisspiraten, Weisse Rose, Kreisauer Kreis, Ludwig Beck, Pastor Niemöller, Carl Goerdeler, Innere und äussere Emigration, Poldi, Dortmund.
Original Klaus Rohde. From Klaus Rohde: Satire, Politik und Kunst. ©Klaus Rohde [1]
| Es gab zahlreiche Aktionen gegen Hitler während der Nazidiktatur. Hier besprechen wir einige der wichtigsten. Viele Kommunisten, Sozialdemokraten und andere Antinazis wurden sofort nach der Machtübernahme durch Hitler in Konzentrationslager gesteckt, lange bevor die Juden öffentlich verfolgt wurden. Die meisten hatten keine “grossen” Namen und sind heute vergessen; ich erwähne einen solchen Fall aus eigener Erfahrung im letzten Beispiel unten. – Personen im Widerstand kamen aus allen Gesellschaftsschichten: Arbeiter und Akademiker, evangelische und katholische Geistliche, Offiziere und Studenten, Kommunisten und Sozialdemokraten, Republikaner und Monarchisten. – Viele sahen anfangs Hoffnung im Nationalsozialismus, der den Versailler Vertrag ausser Kraft setzen wollte, und der die Wirtschaftskrise der Grossen Depression, die Deutschland mehr als andere Länder betroffen hatte, zu beenden versprach, doch verloren ihre Illusionen bald.
Georg Elser
http://en.wikipedia.org/wiki/File:Georg_Elser.jpg Public domain Georg Elser, ein schwäbischer Schreiner, versuchte am 8. November 1939 Adolf Hitler im Münchner Bürgerbräukeller in die Luft zu sprengen. Er brauchte Wochen, um eine Säule im Keller auszuhöhlen und mit Sprengstoff zu füllen. Zwei selbstgebaute Auslöser sollten die Sprengladung zu einer vorgegebenen Zeit auslösen. Elser hatte sich vorher darüber informiert, zu welcher Zeit Hitler bei derartigen Versammlungen anwesend war. Alles klappte wie geplant, doch hatte Hitler den Bürgerbräukeller unerwartet früh verlassen und entkam. Elser wurde an der Schweizer Grenze gefasst und nach Foltern und Verhören in das Konzentrationslager Sachsenhausen gebracht. Kurz vor Kriegsende wurde er im Konzentrationslager Dachau auf Hitlers Befehl erschossen. Einzelheiten hier:
Dietrich Bonhoeffer [2]
Kardinal Graf von Galen Clemens August Graf von Galen war Bischof von Münster während des Nazi-Regimes, 1946 zum Kardinal erhoben und 2005 seliggesprochen. In seinen Predigten machte er wiederholt seine Opposition gegen Euthanasie, erzwungende Sterilisierung, Konzentrationslager und die nationalsozialistische Erziehungspolitik klar. Seine Predigten wurden gedruckt und waren weit verbreitet, selbst unter Soldaten an der westlichen und östlichen Front. Er war verantwortlich für das Ende des öffentlichen Euthanasie-Programmes. Er unterstützte jedoch Hitlers Angriff auf die Sowjetunion und hielt die Sowjetunion anscheinend für ein grösseres Übel als die Nazis. Während der letzten Jahre des Nazi-Regimes befand er sich praktisch unter Hausarrest. http://de.wikipedia.or/wiki/Clemens_August_Graf_von_Galen http://www.whoswho.de/templ/te_bio.php?PID=488&RID=1 Edelweisspiraten http://einestages.spiegel.de/static/topicalbumbackground/5105/_wenn_die_hitlerjungen_flitzen.html
Die Weisse Rose (Hans und Sophie Scholl, Christof Probst, Alexander Schmorell, Willi Graf, Professor Kurt Huber) http://www.yolanthe.de/biograf/scholl.htm
Kreisauer Kreis Der “Kreisauer Kreis” war ein Mittelpunkt der Opposition zu Hitler, mit etwa 20 national-konservativen, christlichen und sozialdemokratischen Mitgliedern, zum Teil aus altem preussischem Adel wie Helmuth James von Moltke und Peter Yorck von Wartenburg. Mitglieder waren unter anderem Eugen Gerstenmaier (später in der CDU und Bundestagsvorsitzender) und Julius Leber (Sozialdemokrat,1945 hingerichtet). Der Kreis besass auch zahlreiche Sympathisanten. Man plante die Schaffung einer neuen staatlichen Ordnung für Deutschland für die Zeit nach der Entfernung Hitlers. Es wurde Kontakt mit dem Widerstand in der Armee und anderen Gruppen aufgenommen. Man wollte Hitler absetzen und vor Gericht stellen. Einige Mitglieder schlossen sich später der Operation Walküre an (siehe Claus von Stauffenberg).
General Ludwig Beck
Bundesarchiv Bild 183-C13564, Ludwig Beck.jpg This file is licensed under CreativeCommons AttributionShareAlike3.0Germany Generaloberst Ludwig Beck war Generalstabschef von 1935 bis 1938 (als er zurücktrat). Obwohl er zuerst positiv von Hitler beeindruckt war, versuchte er, die Invasion der Tschechoslovakei zu stoppen und ging selbst soweit, sich mit dem Aussenministerium Grossbritaniens in Verbindung zu setzen und zu überreden, Hitler keine Zugeständnisse zu machen. Das Münchener Abkommen untergrub ihn. 1943 versuchte er zweimal, Hitler umzubringen, aber ohne Erfolg. Generalfeldmarschall Rommel war 1944 zu einem Coup bereit unter der Bedingung, dass Beck Kopf der neuen Regierung würde. Beck war führend daran beteiligt, den Anschlag auf Hitler am 20.Juli 1944 vorzubereiten (siehe Claus von Stauffenberg). Es war geplant, ihn zum Leiter der neuen provisorischen Regierung zu machen. Nach dem Fehlschlag des Anschlages wurde er von General Fromm, dem Führer des Ersatzheeres um Berlin, festgenommen und zum Selbstmord gezwungen (ohne Erfolg, er verwundete sich nur schwer und ein Soldat musste ihn erschiessen). Fromm wurde selbst von Goebbels, dem Gauleiter von Berlin, festgenommen und später hingerichtet.
Pastor Niemöller
Martin Niemöller war ein Patriot, der im ersten Weltkrieg ein U-Boot kommandierte. Die Weimarer Republik beeindruckte ihn nicht und er stand dem Aufstieg Hitlers zur Macht positiv gegenüber. Seine Haltung änderte sich nach einem Treffen zwischen ihm, zwei protestantischen Bischöfen und Hitler, bei dem der politische Druck auf die Kirchen diskutiert wurde. Sein Telefon war von der Gestapo angezapft worden. Im Mai 1934 gründete er und andere die Bekennende Kirche, in Opposition zur staatlich gestützten “Deutschen Reichskirche”. Seine weit zirkulierten Predigten waren Nazi-kritisch. In den folgenden Jahren wurde er mehrfach verhaftet, verbrachte über sieben Monate in Einzelhaft, wurde vor Gericht gestellt und verurteilt, und in die Konzentrationslager Sachsenhausen und Dachau gebracht. Er wurde erst am Ende des Krieges befreit. http://www.kirchenlexikon.de/n/niemoeller_m.shtml
Carl Goerdeler http://de.wikipedia.org/wiki/Carl_Friedrich_Goerdeler
Carl von Ossietzky Carl von Ossietzky war ein deutscher Journalist und radikaler Pazifist, der schon vor Ausbruch der Ersten Weltkrieges, aber insbesondere nach seiner Teilnahme an der Schlacht um Verdun, während und nach dem Krieg aktiv gegen den Krieg propagierte, zuletzt als Chefredakteur der einflussreichen Zeitschrift “Weltbühne”. Schon vor der Machtübernahme durch die Nazis wurde er wegen der Verrates militärischer Geheimnisse gerichtlich verurteilt. Er lehnte die Auswanderung nach der Machtübernahme durch die Nazis ab, wurde 1933 nach dem Reichtstagsbrand von der Gestapo verhaftet und gefoltert, und in ein Konzentrationslager eingeliefert, wo er sich eine schwere Tuberkulose zuzog. 1936 wurde er in ein polizeiliches Krankenhaus überstellt. 1936 wurde ihm der Friedensnobelpreis rückwirkend für 1935 verliehen, eine kontroverse Verleihung, sogar von vielen Leuten in Norwegen, auch dem König , verurteilt (der König lehnte es ab, an der Verleihungszeremonie teilzunehmen). Die Nazis erlaubten ihm zwar, den Preis anzunehmen, er durfte zur Entgegennahme des Preises aber nicht nach Oslo reisen. Als Folge der Verleihung an Von Ossiezky ordnete Hitler an, dass kein Deutscher einen Nobelpreis mehr annehmen dürfe. 1938 starb Von Ossietzky als Folge der Folterungen und Tuberkulose, noch immer im Krankenhaus unter Polizeiaufsicht stehend. Innere und Äussere Emigration Besonders aktiv im Ausland waren unter anderem Fritz Lang und Bertolt Brecht, die in den USA gemeinsam den Film “Hangmen Also Die” drehten, Heinrich Mann, der schon in Paris zum Ehrenvorsitzenden des “Schutzverbandes Deutscher Schriftsteller” und zum Präsidenten der “Deutschen Freiheitsbibliothek” berufen wurde, Oskar Maria Graf, der öffentlich dagegen protestierte, dass seine Bücher nicht mit denen anderer verboten und verbrannt wurden (was dann in der Universität München nachgeholt wurde), und Klaus Mann, der besonders durch seinen auch verfilmten Roman Mephisto berühmt wurde, in dem die Karriere eines genialen Schauspielers (Gustaf Gründgens) unter den Nazis dargestellt wurde. Unter den in Deutschland verbliebenen musste Carl von Ossietzky einige Zeit im Konzentrationslager zubringen und Erich Kästner wurde mit Schreibverbot belegt. Aber auch einige Prominente, die sich mit dem Regime arrangiert hatten, halfen in individuellen Fällen Antinazis, dem schlimmsten zu entkommen. Gustaf Gründgens[16], der wohl berühmteste Schauspieler und Regisseur der Nazizeit, half dem von der Gestapo gefassten kommunistischen Schauspieler und Sänger Ernst Busch unter erheblichen Risiko für sich selbst, der Todesstrafe zu entgehen. Poldi Die bisher besprochenen Beispiele behandeln Personen, die entweder durch spektakuläre Aktionen oder exponierte Positionen als besonders wichtig gelten. Die grosse Mehrzahl der Widerständler waren aber kleine Leute, die bald aus der Vorstellungswelt der Normalbürger verschwanden. Kommunisten und Sozialdemokraten waren der Aufmerksamkeit der Nazibehörden besonders sicher, aber auch viele andere handelten aufgrund ihrer Überzeugung gegen die Nazidiktatur. Ich stelle einen Fall aus meiner eigenen Erfahrung dar, und zugleich auch, wie sich das Leben zu jener Zeit in den Augen eines Kindes und Jugendlichen darstellte. Übrigens: ich war kurz vor Ende des Krieges 13 Jahre alt geworden, also in einem Alter, wo man vieles durchaus klar sehen konnte und verstand. Was spielte sich so ab, und was sah man vom Widerstand? Poldi ist der Spitzname,dem wir unserem neuen (1945) Geschichtslehrer gaben. Er hatte mehrere Jahre im Zuchthaus Brandenburg zugebracht. Wir hörten (ich kann das aber nicht dokumentarisch belegen), dass er Feldwebel gewesen sei und bei Anfang des Krieges vor der Truppe gesagt haben soll: “Wenn wir diesen Krieg gewinnen wollen, müssen wir erst die SS loswerden”. Man machte ihmden Prozess und er wurde zum Tode verurteilt, dann aber zu lebenslänglicher Haft begnadigt. Er starb nach einigen Jahre an einer Tuberkulose, die er sich während der Haft zugezogen hatte.Dies also in memoriam Poldi, als Stellvertreter der tausenden oder zehntausenden oder hunderttausenden kleinen Leute, die es wagten, aufzumucken und dafür zahlen mussten. Widerstand viel weiter verbreitet als oft angenommen (Beispiel Dortmund) Josef Alvermann, Baden-Baden, hat mir erlaubt, seinen Kommentar (siehe Comments) auch hier einzufügen: Ohne auch nur auf die zahlenmäßige Größe des Widerstands hinzuweisen, berichten Funk, Fernsehen und Presse leider fast immer nur über dieselben Widerstandskämpfer, die sich auch publicitymäßig von ihren vielen gleich mutigen Leidensgenossen hervorheben. Daher kennt die Öffentlichkeit fast nur sie, so dass der unbefangene Leser vor allem im Ausland annehmen muss, tatkräftiger Widerstand sei eine Sache weniger Menschen gewesen, vorwiegend individualistischer ‘Freidenker’, militärischer (Planck, Rommel), elitärer (von Stauffenberg), kirchlicher (Niemöller, Bonhoeffer) oder mutiger unvorsichtiger Einzelner (wie Poldi.) In Wirklichkeit gab es beispielsweise in der damals 340 000 Einwohner zählenden Stadt Dortmund neben der organisierten kommunistischen Gegnerschaft und ähnlichem sozialdemokratischen Widerstand (Ortsgruppenleiter Josef Leinberger wurde in Dachau ermordet) die unterschiedlichsten Gruppierungen, die im Untergrund tätig waren. Ich erwähne die illegalen Gruppen der Naturfreunde sowie den Freien Wanderbund, den Kreis um den Arbeitersport, aus dem sich August Braun mit einer Handgranate in die Luft sprengte, als die Gestapo ihn verhaften wollte, und die über hundert Mitglieder zählende Gruppe Winzen, die sich aus der Freidenkerjugend rekrutierte, deren Vordenker Paul Winzen und Josef Kasel in Plötzensee hingerichtet wurden, wo allein 3000 Widerständler in den langen 12 Jahren des Tausendjährigen Reichs ihr Leben ließen. Darüberhinaus wurden von den vielen hunderten verurteilter Dortmunder Widerstandskämpfer rund einhundert in Konzentrationslager eingewiesen, deren Terror fünfundzwanzig nicht überlebten. Doch auch die genauen Unterlagen der Bürokratie geben nicht einmal über die hingerichteten Widerstandskämpfer vollständig Auskunft. Allein in Dortmund wurden im Rombergpark noch nach Kriegsende (19. 4. 45) fünfundzwanzig durch Genickschuss getötete Personen gefunden, darunter eine Frau und der blinde Paul Pietzko (mit Blindenhund), der als Verbindungsmann zu Dortmunder Kommunisten tätig war. – Rechnet man zu den vielen entdeckten die wohl nicht seltenen unentdeckt gebliebenen Widerständler hinzu und gar die vielen Fälle, von denen die Überlebenden des 3. Reichs achtungsvoll sprachen, dass Augen- und Ohrenzeugen tapferer Worte und Handlungen (im Gegensatz zum Fall Poldi) die Sache mutig übergingen und verschwiegen, so ergibt sich ein ganz anderes Bild. Wir Heutigen leben in Staaten, in denen niemand vergleichbare heroische Taten vollbringen muss, doch etwas mehr Zivilcourage, um gegen die Auswüchse unserer Gesellschaft und mafiaartige Machenschaften anzugehen, wäre sehr nützlich und würde zugleich den seltenen Mut der Gegner des Naziterrors ehren. Literatur: Stadt Dortmund, Stadtarchiv (1981) “Widerstand und Verfolgung in Dortmund 1933-1945″. Zweite Auflage, 336 Seiten, 1040 Abbildungen. Eine Dauerausstellung in Dortmund befasst sich ebenfalls mit diesem Thema. |
There were numerous instances of resistance against Hitler during the Nazi dictatorship. Here we discuss some of the most important ones. Many communists, social democrats and other anti-Nazis were put into concentration camps more or less immediately after Hitler took over power, long before the open persecution of jews. Most had no “great” names and are today forgotten; I mention such a case as the last example below. – Persons in the resistance were from all layers of society: workers and academics, protestant and catholic clergy, officers and students, communists and social democrats, republicans and monarchists. – Many looked at first with some hope at National Socialism, which promised to abrogate the Treaty of Versailles and to end the economic crisis of the Great Depression, which had affected Germany more than other countries, but soon lost their illusions. A brief overview on the German resistance in English can be found here.Georg ElserGeorg Elser, a Swabian carpenter, attempted to blow Hitler up in the Munich Bügerbräukeller on 8 November 1939. It took him weeks to hollow out a pillar in the cellar (a pub) and to fill it with explosives. Two self-made triggers were supposed to release the explosion at a pre-set time. Elser had previously gathered information about the time at which Hitler was always present at such meetings. Everything went according to plan, but Hitler left the Bürgerbräukeller unexpectedly early and escaped. Elser was captured at the Swiss border and transferred to the concentration camp Sachsenhausen after torture and interrogations. He was shot on Hitlers orders shortly before the end of the war in the concentration camp Dachau. Details here: http://www.spiegel.de/international/germany/0,1518,586094,00.html http://user.cs.tu-berlin.de/~schwartz/pmh/elser/vita.html http://www.gdw-berlin.de/bio/ausgabe_mit-e.php?id=24
Dietrich Bonhoeffer
public domain: Dietrich Bonhoeffer was a Protestant pastor and leading in the “Bekennende Kirche” (Confessing Church). The Church expressedly stated that NS race ideology was incompatible with Christianity. Bonhoeffer was anti-Nazi from the beginning but became actively involved in overthrowing the regime in 1940, using his international connections. He was arrested in 1943, sentenced to death and executed for resistance activities in April 1945, together with Admiral Wilhelm Canaris (Head of Military Intelligence), General Hans Oster and Hans von Donanyi. http://www.iep.utm.edu/bonhoeff/
Kardinal Graf von Galen
Public domain http://en.wikipedia.org/wiki/Clemens_August_Graf_von_Galenhttp://www.gdw-berlin.de/bio/ausgabe_mit-e.php?id=274 Clemens August Graf von Galen was Bishop of Münster during the Nazi-regime, became a Cardinal in 1946 and was blessed in 2005. In his sermons he repeatedly stated his opposition to euthanasia, forced sterilization, concentration camps, and Nazi-measures in education. His sermons were reproduced and circulated widely, even among soldiers at the Western and Eastern fronts. He was responsible for the end of the open euthanasia program. However, he supported Hitler’s invasion of the Soviet Union and generally seems to have considered the Soviet Union as a greater evil than the Nazis. For the last years of Nazi rule he was under virtual house arrest. Claus von Stauffenberg
Claus von Stauffenberg was an army officer who was at first favourably impressed by Hitler. He turned radically against him after the anti-Jewish progrome in 1938 (the “Kristallnacht”) and was a leading figure in the movement to remove Hitler, the “Operation Walküre”. For this purpose he was in contact with other members of the resistance including General Ludwig Beck and Carl Goerdeler. During an arial attack in North Africa he had lost his right hand, his left eye and two fingers of the left hand, a fact which somewhat hampered the assassination attempt later. On 20 July 1944 he planted a bomb very close to Hitler at the Führerhauptquartier, the “Wolfsschanze”, in East Prussia. He left the room, the bomb exploded and he flew to Berlin convinced that Hitler was dead. However, Hitler survived, Stauffenberg and others were caught and shot. Erwin Planck, the son of Max Planck, among many others, was also executed [4] . http://www.spartacus.schoolnet.co.uk/GERstauffenberg.htm
Edelweisspiraten Edelweisspiraten is a collective term for various youth groups which did not like the reglemented activities of the Hitler Youth and the BDM (Union of German Girls) and often had street fights with them. They wore Edelweiss badges, apparently in mockery of Hitler (Edelweiss was Hitlers favoured flower), and local groups tended to use different names. In some cases they also engaged in anti-Nazi activities by distributing, for example, anti-Nazi propaganda and helping army deserters. Towards the end of the war several of them were executed in Cologne. Many continued their activities after the war, sometimes directed against the occupying powers. In the Soviet zone membership in the Edelweisspiraten was automatically punished by long-term imprisonment. http://en.wikipedia.org/wiki/Edelweiss_Pirates
Die Weisse Rose (Hans und Sophie Scholl, Christof Probst, Alexander Schmorell, Willi Graf, Professor Kurt Huber) Hans und Sophie Scholl were at first positively impressed by National Socialism and Hans even took part in the Parteitag der NSDAP (the annual national meeting of the Nazi party) in Nürnberg 1935. However, under the impression of the Parteitag he resigned from the HJ (the Hitler Youth) and joined instead the illegal Deutsche Jungenschaft 1.11. Hans and Sophie Scholl were captured by the Gestapo in 1937 and Hans was imprisoned for five weeks. As students at the University of Munich they later met Christof Probst, Alexander Schmorell und Willi Graf. They distributed anti-Nazi pamphlets (the “White Rose”) and published five editions of it in 1942/43. Professor Kurt Huber also joined the group.They were captured by the Gestapo while distributing the 6th edition, sentenced to death on 22 February 1943 and immediately executed. http://www.historyplace.com/pointsofview/white-rose1.htm http://hs.riverdale.k12.or.us/~dthompso/german/wrose/
Kreisauer Kreis
The Kreisau Circle was a centre of opposition to Hitler, with about 20 national-conservative, Christian and social democratic members. Some belonged to the old Prussian aristrocracy like Helmuth James von Moltke and Peter Yorck von Wartenburg. Others included for example Eugen Gerstenmaier (later in the CDU = Christian Democratic Party, and Chairman of the Bundestag = Federal Parliament) and Julius Leber http://en.wikipedia.org/wiki/Kreisau_Circle
Pastor Niemöller
Public domain. http://www.ushmm.org/wlc/article.php?lang=en&ModuleId=10007391 Martin Niemöller was a patriotic German, commandant of a U-boat in the First World War. He was not impressed by the Weimar Republic and favoured the rise of Hitler to power. His attitudes changed at a meeting of himself, two Protestant bishops and Hitler, at which political pressures on the churches were discussed. His telephone had been tapped by the Gestapo, and he now opposed the Nazi dictatorship. In May 1934 he and others formed the Confessing Church, in opposition to the state sponsored “Deutsche Reichskirche”, and his widely known sermons were very critical of the Nazis. In the following years he was arrested several times, spent over seven months in 1937 in solitary confinement, put on trial and sentenced, and put into the Sachsenhausen and later the Dachau concentration camps. He was liberated at the end of the war.
Carl Goerdeler
http://www.spartacus.schoolnet.co.uk/GERgoerdeler.htm http://www.gdw-berlin.de/bio/ausgabe_mit-e.php?id=30 The conservative-monarchistic Carl Friedrich Goerdeler was Lord Mayor of Leipzig from 1930-1937. He resigned in protest when the memorial to Felix Mendelssohn-Bartholdi in Leipzig was removed at the end of 1936. He used trips abroad to propagate against the Nazis. At the outbreak of war his activities increased, leading to the formation of the “Goerdeler-circle”, a centre of resistance to Hitler, with contacts to other resistance groups. After the failure of Operation Walkyrie on 20 July 1944 he was tried and sentenced to death. Execution followed in February 1945.
Carl von Ossietzky
 ADN-ZB http://en.wikipedia.org/wiki/Carl_von_Ossietzky http://www.dhm.de/lemo/html/biografien/OssietzkyCarl/index.html Carl von Ossietzky was a German journalist and radical pacifist who, even before the beginning of the First World War, but especially after fighting at Verdun in the war, actively wrote against the war, in his last years as editor of the influential journal “Weltbühne”. Even before the Nazis came to power, he was tried in court for publishing military secrets. He refused to emigrate after the Nazis came to power, and was imprisoned and tortured in concentration camps by the Gestapo in 1933, after the burning of the Reichstag. After contracting a serious tuberculosis, he was transferred to a hospital run by the secret police in 1936. He was awarded the Nobel Prize for peace retroactively for 1935 in 1936, a controversial award, condemned even by many people including the king in Norway, who refused to attend the award ceremony. The Nazis allowed him to accept the prize, but he was not allowed to travel to Oslo to receive it. As a consequence of the award to Von Ossietzky, Hitler ordered that Germans could not accept future Nobel prizes. Von Ossietzky died in 1938 as a consequence of torture and tuberculosis, still in hospital under police observation. |
An Ethical Basis for Nature Conservation: Arthur Schopenhauer
In the last chapter of the book edited by me “The Balance of Nature and Human Impact, Cambridge University Press 2013″, we, i.e. Klaus Rohde, Hugh Ford, Nigel R.Andrew and Harold Heatwole” deal with “How to Conserve Biodiversity in a Nonequilibrium World”. The first section of the chapter discusses economic, esthetic and ethical arguments for conserving biodiversity. We conclude that in the modern world people are most impressed by economic arguments, whereas the ethics of the problem is very rarely considered. Are there ethical reasons for conserving biodiversity? We point out that there indeed are, convincingly demonstrated by the German philosopher Arthur Schopenhauer. His philosophy is particularly suitable, because it appeals not only to philosophically educated Westerners, but also to all those who have a Buddhist or Hinduistic background, i.e. a very large proportion of mankind. Schopenhauer was the first Western philosopher who taught that ethical (moral) behaviour must be based on compassion with humans and animals.
I have given a concise outline of Schopenhauer’s philosophy of ethics and justice earlier:
https://krohde.wordpress.com/article/arthur-schopenhauer-ethics-and-theory-xk923bc3gp4-106/
Here I mention a few important points in excerpts taken from my earlier essay:
Schopenhauer’s ethics and theory of justice follow from his epistemology, according to which the world as it appears to us, as we perceive it, is to a large degree shaped by our mental apparatus. Following Immanuel Kant, he assumes that time, space and causality are not characteristics of the thing-in-itself (“Ding an sich”) but categories of our mind. All distinctions between individuals disappear once these categories are taken away. In other words, all beings are in essence One.
Schopenhauer’s ethics has had a deep influence on many philosophers and writers after him. Albert Einstein, for example, mentions Schopenhauer as an important influence on his views. Schopenhauer was the first who arrived at conclusions similar to those in Eastern philosophy, in particular Hinduism and Buddhism. And he was the first in Western philosophy who based ethics on compassion with man and animals.
……… Schopenhauer develops a theory of ownership, of natural justice and law in general. Injustice is the original and positive, justice the derived and negative concept. “The only purpose of law is determent from encroaching on others’ rights”. Schopenhauer considers Kant’s thesis that humans should always be considered to be the end (“Zweck”) and never as means, as vague and problematic, because “a murderer sentenced to death must with full justification be used as means”, as a determent and for the re-establishment of public security. However, this applies only to justice in time (“zeitliche Gerechtigkeit”), eternal justice which applies to the entire world (that is, lies in its essence) and does not depend on human constructions (“Einrichtungen”), cannot be retaliatory, because it lies not in time unlike justice in time which is based on retaliation. “Punishment must here (in eternal justice) be connected with the crime in such a way that both are one.” If one wants to know what humans as a whole and in general are worth from a moral perspective, one only has to look at their fate as a whole and in general. This is indigence (“Mangel”), misery, agony and death. Eternal justice at work…..”. However, the “crude individual” has a different view, since he knows only the temporally and spatially separate appearances: he sees tormentors and murderers on the one side and sufferers and victims on the other, who are really only One. Nevertheless, in the depth of his consciousness he sometimes has the “somewhat dark hunch” that “all this is not entirely foreign to him”. Horror (“Grausen”) is founded on this sometimes appearing hunch. All evil in the world derives from the Will which is the real essence of each single person. Hence (Schopenhauer quotes Calderon’s “Life as Dream”, in which the Christian dogma of original sin is expressed: “Since the greatest guilt of man is that he was born”). – Esoterically depicted in the Vedas and especially in the Upanishads, the myth of transmigration expresses the cognition of eternal justice in an easily understandable form for the people. You must not kill an animal, because at a time in eternity you will be born as such an animal and suffer the same death”. This is the meaning of “tat twam asi” (This is you), which is the foundation of Hindu teaching. – In the same sense Christian ethics forbids retaliation of evil with evil and submits to eternal justice (“Revenge is mine, I shall retaliate, says the Lord”).
Our discussion to this point permits a description of the ethical significance of action. According to Schopenhauer, genuine virtue can come only from the insight which recognizes in a foreign being the same being as one’s own. “In principle (“an sich”) all deeds…. are just empty images, and only the attitude (ethos, “Gesinnung”) that leads to them, lends them moral significance.” The principle of justice (based on the negation of evil) commands that one must not hurt others.” Genuine goodness goes much further and leads to love of mankind (“Menschenliebe”): one distinguishes much less than usually between oneself and others, one sacrifices one’s property and even oneself to one’s neighbour (“Nächster”) and one does not torture an animal. Love is based on the recognition of foreign suffering and pure love is therefore by its nature compassion. All this is in direct contradiction to Kant’s view that any truly good and virtuous deed is based on abstract reflection, on the concept of duty and the categorical imperative.
In Schopenhauer’s time (the first half of the 19th century), destruction of the environment had not become the important issue it is today. Hence, he does not deal with conserving the environment as such. However, his conclusion that moral behaviour of humans must be based on compassion with fellow humans and animals should be interpreted as meaning that animals must be protected and therefore also their habitats and the environment in general. In other words, we must not preserve organisms and the environment as a whole because they are of economic benefit to us, we must conserve them because we have an ethical responsibility towards nature, i.e., not only to the next generations of humans, but also to other living beings.
Freedom of speech in Australia 2015
Where is the limit of free speech in a Western democracy? A recent example.
Since the Liberal-National took over government with Tony Abbott as Prime Minister in 2013, worrying trends have emerged to make media reporting even more one-sided than it already had been. Two thirds of printed media are controlled by Rupert Murdoch (of Fox News in the USA fame), whose reporting is ridiculously one-sided, supporting right-wing economics and politics, but this was to a certain degree balanced by the two public broadcasters, ABC and SBS, which followed a more or less “neutral” line. The Liberal/National government, soon after taking office, reduced funding for the two public broadcasters, leading to the dismissal of many staff, changed the rules with the intention of making government appointed members of he boards more directly responsible for broadcasting policy, and forced the broadcasters to rely more on private advertising. Most recently, the Minister for Communications, Malcolm Turnbull, “drew attention” of the Chairman of SBS to some tweets by Scott McIntyre, a prominent sports-commentator employed by SBS. He claimed not to have asked for the firing of McIntyre, but the result was that he was immediately fired, without discussion, without warning. What were these “offensive” tweets?
ANZAC day commemorations throughout Australia, which commemorate the landings at Gallipoli, Turkey, in 1915, by morning services in (more or less) all towns, even small ones, by marches, flights of airforce jets etc. were particularly elaborate this year, the 100th anniversary of the beginning of the failed campaign which led to 10,000’s of deaths of British, Australian, New Zealand, French, Indian, Canadian soldiers, as well as over 90,000 deaths on the Turkish side. They were the culmination of months of almost daily reporting on the first world war, with stories of heroism etc. on t.v. and in the printed media. Scott McIntyre did not like this reporting and published some tweets objecting to it.
According to The Australian, a Murdoch-run newspaper, 27.4.2015:
“An SBS presenter has been sacked over a vicious public attack on Australian Diggers in which he implied that Anzacs were rapists and terrorists. SBS managing director Michael Ebeid labelled the remarks inappropriate and disrespectful, saying they breached the broadcaster’s code of conduct and social media policy. “It’s not tenable to remain on air if your audience doesn’t respect or trust you,” he said. Soccer reporter Scott McIntyre, who has a Twitter following of 30,000 people, shocked followers with a post which implied that Australians commemorating Anzac Day were “poorly-read … drinkers and gamblers”.
He began his tirade about 5pm, calling Australia’s involvement in the World Wars an “imperialist invasion of a foreign nation”.
Later tweets read: “Wonder if the poorly-read, largely white, nationalist drinkers and gamblers pause today to consider the horror that all mankind suffered.” “Remembering the summary execution, widespread rape and theft committed by these ‘brave’ Anzacs in Egypt, Palestine and Japan,” said another post.”
Here are his tweets as reported by some newspapers:
“The cultification of an imperialist invasion of a foreign nation that Australia had no quarrel with is against all ideals of modern society.”
“Wonder if the poorly-read, largely white, nationalist drinkers and gamblers pause today to consider the horror that all mankind suffered.”
“Remembering the summary execution, widespread rape and theft committed by these ‘brave’ Anzacs in Egypt, Palestine and Japan.”
“Not forgetting that the largest single-day terrorist attacks in history were committed by this nation & their allies in Hiroshima & Nagasaki”
“Innocent children, on the way to school, murdered. Their shadows seared into the concrete of Hiroshima”
According to The Australian, “The tweets sparked outrage from Australian leaders, including Communications Minister Malcolm Turnbull who labelled his comments “despicable”. “Difficult to think of more offensive or inappropriate comments,” Mr Turnbull tweeted. “Despicable remarks which deserve to be condemned.””
“SBS issued a statement today from its managing director Mr Ebeid and its sport director Ken Shipp that McIntyre had been sacked: “Late on Anzac Day, sports presenter Scott McIntyre made highly inappropriate and disrespectful comments via his twitter account which have caused his on-air position at SBS to become untenable,” the statement read.
“Mr McIntyre’s actions have breached the SBS Code of Conduct and social media policy and as a result, SBS has taken decisive action to terminate Mr McIntyre’s position at SBS, with immediate effect.”
According to The Guardian, 27.4. 2015, “However, some criticised SBS for firing McIntyre, including journalist Hugh Riminton, who is also a board member of Soldier On, an organisation that supports injured soldiers. Riminton said the tweets were untimely, immature and in one case offensively wrong. “But lest we forget, our diggers also died for free speech,” he said.
The human rights commissioner, Tim Wilson, said McIntyre’s freedom of speech was not being curtailed.
“We’re talking about political interpretations of history and that is open for debate,” he said. “And he will be judged very harshly.”
Most comments in various newspapers strongly condemned McIntyre and did not object to his dismissal. For example, the comedian Merrick Watts wrote: “Today’s comments by @mcintinhos are as sad as they are ill informed. Gutless. Stupid. Disgraceful. I am truly furious.”
According to The Guardian, McIntyre had not deleted his tweets by Sunday morning and had favourited several which supported his views including one that said: “Good on you @mcintinhos for posting this. Usual twitter shit storm, as one would expect, from white Aussie bogans.”
Interestingly, a professor of journalism said that McIntyre had the right to free speech but not to keep his job for it.
John Pilger, the well known Australian writer living in Britain, strongly defended McIntyre’s remarks and agreed with the essence of them. Here are some excerpts of an article published in the Sydney Morning Herald 29.4.2015, in which he “saluted not only Scott McIntyre but also the aboriginal freedom fighter Ray Jackson:
“He exposed cynical drivel by offending in the best tradition of freedom of speech.” “Aboriginal campaigner shone a light on deaths in custody for 30 years. Following a week in which the words “heroes” and “heroism” bobbed on a tsunami of raw propaganda, a tribute is due to two unrecognised Australian heroes. The first is Ray Jackson, who died on April 23.
Ray spoke and fought for a truth…… He said this was a land not of brave Anzac “legacies”, but of dirty secrets and enduring injustices that only a national cowardice could sustain. “Conformity is widely understood and obeyed in Australia,” he wrote to me, “freedom is not……… Australia incarcerates black Australians at a higher rate than that of apartheid South Africa……Ray loathed warmongering and would approve of my second hero. This is Scott McIntyre, the young SBS soccer journalist who, in four now famous tweets, set out to counter the authoritarian sludge that demands we celebrate the criminal waste of life in the British imperial invasion of Turkey a century ago, rather than recognise unpalatable truths about our past and present……..Why? Australia, a nation without enemies, is spending $28billion a year on the military and war and armaments in order to fulfil a tragic, entirely colonial and obsequious role, as Washington’s “deputy sheriff”……..
Scott McIntyre drove the Twitter equivalent of a five-ton truck through such maudlin, cynical drivel. He tweeted the unsayable, much of it the truth; and all decent journalists – or dare I say, freedom-loving Australians – should be standing up for him. That Malcolm Turnbull, who made his name unctuously shouting about freedom of speech, should have been involved in the saga with McIntyre’s employer, SBS, in whatever form, is a measure of the state of public and media life in Australia.
That a journalism professor of long standing, John Henningham, can tweet that “freedom of speech meant that journalists had the right to speak without breaking the law but did not have the right to keep their job when offending others” is a glimpse of the obstacles faced by aspiring young journalists as they navigate the university mills.
Many young people reject this, of course, and maintain their sense of the bogus, and McIntyre is one of them. He offended in the highest tradition of freedom of thought and speech. Knowing the personal consequences would be serious, he displayed moral courage. When his union – the MEAA – locates its spine and its responsibility, it must demand he is given his job back. I salute him.”
Professor Gillian Triggs, the Human Rights Commissioner, who a number of weeks ago was asked by the Attorney General to resign from her post because she had criticized the government’s policy concerning children in detention, but refused to do so, is a very distinguished academic lawyer. Her opinion on freedom of speech in Australia, arising from the sacking of a sports reporter by the SBS for tweets he had published on his personal twitter account, was published in Fairfax newspapers including The Age (Melbourne) and The Sydney Morning Herald (Sydney).
Some excerpts:
“The disciplining or sacking of employees whose emails breach industry codes of conduct – most recently of Scott McIntyre, who alleged crimes by the Anzacs – raise the vexed question of the proper constraints on freedom of speech. Does an employer have the right to sack, demote or otherwise sanction an employee for speech that both breaches its code of conduct and may be substantially inaccurate, in bad faith and deeply hurtful to most Australians?”
“Ask any citizen if they have a right to freedom of speech and they will robustly assert “yes, of course” . However, under Australian law, there is no such formal legal right. While, in practice, everyone is free to say and write whatever they like, this freedom is significantly qualified by exceptions. Prohibitions abound in respect of statements that are libellous or slanderous, in contempt of court, a breach of copyright, obscene or seditious, or that incite mutiny, commission a crime or disclose official secrets.”
“It is probable that …….. decision reflects Australian law in the absence of any legislation confirming the common law right to freedom of speech. While we may say what we please, subject to defined prohibitions, a practical, chilling outcome of freedom of speech is that we must suffer the consequences if that speech is also a breach of an employment contract.”
“……. Public officials, government agencies and contracted service providers will be guaranteed anonymity and immunity if they disclose an abuse of public trust, corruption, acts that endanger the environment, or unjust, oppressive or negligent conduct, among other wrongs. However, the act is significantly limited and does not cover judicial conduct, ASIO or ASIS, politicians or the private sector.
Scott McIntyre may not have the benefit of the “whistleblower’s” law, but it is at least arguable that to be peremptorily sacked is disproportionate to the reasonable interests of his employer. These are matters of judgment in light of all the circumstances.”
Concerning the truth of what Scott McIntyre wrote, see the article by Professor Philip Dwyer, Director of the Centre for the History of Violence, School of Humanities and Social Science at the University of Newcastle:
https://theconversation.com/anzacs-behaving-badly-scott-mcintyre-and-contested-history-40955?utm_medium=email&utm_campaign=The+Weekend+Conversation+-+2707&utm_content=The+Weekend+Conversation+-+2707+{0}CID_3c5b7c063d17861725846adb514b29fe&utm_source=campaign_monitor&utm_term=Anzacs%20behaving%20badly%20Scott%20McIntyre%20and%20contested%20history
Returning to our question at the beginning of this post “Where is the limit to free speech in a Western democracy?”, the example discussed seems to suggest that for journalists there is such a limit, at least if they do not want to lose their job. Is this acceptable? Should an academic, for example, fear for his job because he/she publishes posts with which the university does not agree? I know of a case in which an Australian academic was asked by his university to remove a post in which he had criticized the teaching of homeopathy (for which there is no scientific evidence) at his university, which had plans to introduce such a course.
Third book review of Klaus Rohde ed., The Balance of Nature and Human Impact, Cambridge University Press 2013.
The third review of the book edited by me has just been published in Biological Conservation 182, 281-283 (February 2015)
Reviewer is Brian Drayton, TERC Cambridge, MA, USA, who gave me permission to use excerpts from his review.
For earlier reviews see here:
https://blog.une.edu.au/klausrohde/2013/11/10/review-of-klaus-rohde-ed-the-balance-of-nature-and-human-impact-cambridge-university-press-2013/
https://blog.une.edu.au/klausrohde/2013/12/17/2nd-book-review-of-klaus-rohde-ed-the-balance-of-nature-and-human-impact-cambridge-university-press-2013/
This latest review covers two books:
Green Equilibrium: The Vital Balance of Humans and Nature, Christopher Wills. Oxford University Press (2013). xxviii+280 pp.,
and The Balance of Nature and Human Impact, Klaus Rohde (Ed.) Cambridge University Press (2013). xvi+413 pp.
Excerpts dealing with the book edited by me follow:
“These two books make good companions, and it is instructive to read them side by side. In doing so, the reader can reflect upon a central challenge to conservation science, and to the societies within which it carries out its business.”
……………..
“Klaus Rohde’s fascinating edited volume The Balance of Nature and Human Impact offers a snapshot of current research, exploring
evidence for or against equilibrium processes from an array of systems, interspersed with reviews of literature on selected topics. A brief gallop through the table of contents can only suggest its wealth of provocative entries.
Part I: ‘‘Nonequilibrium and equilibrium in populations and metapopulations’’ examines reef fishes ……..
ectoparasites on terrestrial hosts …….. and marine parasites. Part II: “Nonequilibrium and equilibrium in communities’’ examines plankton communities ……, community stability in relation to fire ……., marine and freshwater ectoparasite communities ….. and small mammal ectoparasites …. , and bird populations and communities. Part III addresses ‘‘Nonequilibrium and equilibrium on geographical scales’’ in the context of island flora and fauna …… and arctic vascular plant diversity and spatial variation ……… Part IV: ‘‘Latitudinal gradients’’ focuses on diversity gradients…..reviews the literature providing evidence for and against equilibrium and nonequilibrium explanations,” and ‘‘effective evolutionary time.’’
Part V: ‘‘Effects due to invasive species, habitat loss and climate change’’ is by far the largest section. …….. the section marks a transition, as all the rest of the book looks at ‘‘biocomplex’’ (coupled humannonhuman)systems—where the nonhuman component may include insects … coral reefs ….. , emerging infectious diseases ……., human impacts on biodiversity …… , amphibians …….. , and reptiles ……. Part VI: ‘‘Autecological studies’’ comprises two articles: ‘‘Autecology and the balance of nature—ecological laws and human-induced invasions’’ …… and ‘‘The intricacy of structural and ecological adaptations: micromorphology and ecology of some Aspidogastrea’’.
Part VII: ‘‘An overall view’’ sets much of the foregoing into a larger theoretical and practical context, coming back to the
challenges faced by conservation biology in a world in at least one kind of chronic disequilibrium: anthropogenic climate change. Rohde discusses interspecific competition as a regulator of communities, and the status of evolutionarily stable strategies. Finally, Rohde and co-authors discuss ‘‘How to conserve biodiversity in a nonequilibrium world.’’ Here we come to the crux of the matter. As Wallington et al. (2005) argue, much conservation strategy betrays an underlying ‘‘balance’’ orientation, which often takes the form of creating reserves and assuming that they will ‘‘do the job’’……….; or of reintroducing species or otherwise restoring a system, and then assuming that short-term success will last (also not a safe assumption……………. Rohde et al. argue cogently that in the world we now inhabit, equilibrium assumptions will result in deep design weaknesses in many conservation strategies, and the kind of reflective research represented by this volume as a whole must result in substantial innovation.”
……………
“Both books under review make the case ……. that the unexamined assumption of ‘‘balance’’ has contributed to many of our current ecological crises, and inhibits proper responses to them. In some cases, a naive reading of ‘‘balance’’ contributes to the assumption that in time, any disturbance caused by human activities will be remedied by Nature as it comes back into balance. In other cases, the ‘‘balance of nature’’ is reified without sufficient understanding of ecological systems and their dynamics, so that intended remedies result in further, different disturbance or even system transformation. Our challenge …….. is to convey a much richer, but perhaps just as satisfying, understanding of the way things work, and the implications of that understanding for what conservation must become. As Donald Worster (1994) wrote in his seminal treatment: ‘‘It is a pattern of behavior based on the idea that preserving a diversity of change ought to stand high in our system of values, that promoting the coexistence of many beings and many kinds of change is a rational thing to do. . . .Such a strategy of trying to conserve a diversity of changes may seem paradoxical, but it is founded on a crucial and reasonable insight. We may have to live with change, may even be the products of change, but we do not always know—indeed, we cannot always know—which changes are vital and which are deadly.’’
Australian universities: cracks open up in the ivory towers. Neoliberal economics at its ugliest
A number of years ago I was sitting in the breakfast room of a hotel in Münster/Westphalia next to a German professor, we were talking about the university system in Germany. He dropped some remarks about universities in Australia: “yes, and in Australia degrees are for sale, at least that is what I was told by an Australian colleague.” I was sceptical about that remark, because during my active days at an Australian university I did not encounter cases of degrees for cash. But the situation has changed. Governments have cut funding for universities, funding is based on student numbers, and a large proportion of universities’ funding is supplied by fee-paying foreign students. Foreign students represent one of the largest sources of income for the Australian government. Students expect something (a degree, not necessarily quality) for their money, and so standards have continually been watered down, even at the most prestigious universities. Students have even employed agencies to have their essays written for them and employed people to sit in for them at examinations. And these are not exceptions, such cases are widespread. An article in the Sydney Morning Herald, 22.4.2015 gives a brief and concise overview of what is happening. See here:
Extracts:
Concerning foreign students: ” Fifty per cent of all work submitted now is plagiarised, according to one source – a huge increase on what was happening only five years ago. Students who can barely speak English are initially failed, and then, when their work is re-marked, are given a pass, allowed to register as professionals, and enter the workforce.”
Lecturers “know which students are cheating, and which are plagiarising the work of others; they know whose English is too poor to pass, and who lacks the knowledge or intelligence to graduate. It is when they attempt to act on what they know in an intellectually honest manner, however, that they find obstructions in their way.”
“Decades of government policies in higher education which have destroyed the traditional university as an independent community of scholars and turned it into a degree factory serving the ephemeral interests of the economy are the real cause.”
“The expectation that all courses in all faculties must have some vocational end in view; the destruction of student life with the end of compulsory unionism; the insistence that all research must have immediate practical application – these different trends, all of them market-based, all of them philistine, have all transformed our universities for the worse.”
The government has plans to make the situation even worse by deregulating university fees, i.e. allowing universities to set their own fees in order to get their hands on more cash. These plans have so far been blocked by the Senate, but the government has not given up. Neoliberal economics at its ugliest!
Don’t support science but obscurantism!
If you don’t know the meaning of obscurantism, here it is (from the source of all wisdom, Wikipedia): “Obscurantism (/ɵbˈskjʊərəntɪsm/) is the practice of deliberately preventing the facts or the full details of some matter from becoming known.”
This is what the Australian government is doing, in this case represented by the Minister of Education Christopher Pyne. See here:
It cut many millions of Dollars in funding from the budget of CSIRO, the foremost research organisation in Australia which has done much work on the science of climate change, and many other science projects, but is quite happy to invest four million in a centre to be located at the Business School of the University of Western Australia and devoted to misleading the public (officially “The new centre will focus on applying an economic lens to proposals to achieve good for Australia, the region and the world,” said a statement from UWA).
An extract from the article:
“The government would cover roughly a third of the cost for an Australian iteration of Dr Lomborg’s Copenhagen Consensus Centre at the University of Western Australia (UWA), confirmed Mr Pyne’s office following an investigation by The Guardian Australia.
The news comes on the heels of the Danish economist’s move to the UWA’s school of business and his appointed as Prime Minister Tony Abbott’s advisors on foreign aid.
Labor and environmental activists heavily criticised the appointment, questioning why someone who played down the effects of global warming should be advising on policy concerning developing countries in the Pacific that were exceptionally vulnerable to climate change.”
Dr.Lomborg is not an environmental, but a political scientist and is highly sceptical of the importance of climate change. He has lectured on statistics and the new centre at UWA is in the business and not the science school. He does not deny that climate change is real and human-induced, but thinks it is “not the end of the world”. Climate scientists do not claim that climate change is necessarily “the end of the world”, but Dr.Lomborg’s views differ sharply from those of the vast majority of climate scientists who take the risks much more seriously and want to do something about it. The establishment of the Consensus Centre and the appointment of Dr.Lomborg can only mean that the Liberal-National Government will continue its politics based on the denial of the seriousness of the threat posed by climate change, and shown by the reduction in the clean energy target, the abolishment of the carbon tax, etc.
More about the Copenhagen Consensus Center, the Danish equivalent of the Australan version and run by Dr.Lomborg, and the donors supporting it here:
http://desmogblog.com/2014/06/25/millions-behind-bjorn-lomborg-copenhagen-consensus-center
Australia’s climate change policy all talk and no action
See here:
Extracts:
“The government is refusing to accept a political compromise on the renewable energy target (backed by Labor, the renewables industry and big business) because it thinks the industry won’t be able to reach the target, but the only reason industry wouldn’t reach the target is the absence of a political compromise.”
“The government will set a post-2020 emissions reduction target without a policy to get there.”
“The government is not including climate change in long-term planning exercises that really should be planning for climate change.”
And not to forget: even the term “climate change” appears to be taboo in government papers. It has been replaced by a term which puts much less urgency on the problem: “climate variability”. All in line with the views of Tony Abbott and some of his ministers, who do not take climate change seriously (in Abbott’s word: “crap”).
Put a Prize on Carbon Now!
Have a look at the article linked below.
Extract:
“An international team of scientists has tried a new approach to addressing the complex argument about the costs of climate change – and, once again, the prediction is that the costs of inaction will be so much greater than paying the bills now.
The researchers − from the UK, Switzerland and the US − conclude that policy-makers must apply the brakes and put a high price on carbon emissions “before it is too late”.”
http://www.eco-business.com/news/cut-carbon-now-to-avoid-climate-tipping-points/
The Destruction of Nature
A friend sent me this very useful link:
Overpopulation, overconsumption in pictures
This is where our present economic system has led us and which has to be stopped!
Plastic pollution affects corals
Many studies have shown that enormous quantities of plastic get into the oceans. However, we know little about the effects of plastic on the marine environment. Now, a study by Hall, Berry and Rintoul, published in Marine Biology, has shown that corals, which feed on plankton (beside synthesizing organic matter using symbiotic zooxanthellae) ingest (but do not digest) microparticles of plastic, possibly with severe adverse consequences. For details see here:
http://www.coralcoe.org.au/news/great-barrier-reef-corals-eat-plastic
Full reference here:
Microplastic ingestion by scleractinian corals by N.M. Hall, K.L.E. Berry, L. Rintoul, M.O. Hoogenboom, Marine Biology. DOI 10.1007/s00227-015-2619-7
Amazon rainforest: declining ability to absorb carbon
An article just published in Nature 519, 344-348 (19 March 2015), doi:10.1038/nature14283, shows that the Amazon rainforest’s ability to act as a carbon sink, i.e. to absorb carbon dioxide from the atmosphere, declined over the last decade.
Abstract:
“Atmospheric carbon dioxide records indicate that the land surface has acted as a strong global carbon sink over recent decades, with a substantial fraction of this sink probably located in the tropics, particularly in the Amazon. Nevertheless, it is unclear how the terrestrial carbon sink will evolve as climate and atmospheric composition continue to change. Here we analyse the historical evolution of the biomass dynamics of the Amazon rainforest over three decades using a distributed network of 321 plots. While this analysis confirms that Amazon forests have acted as a long-term net biomass sink, we find a long-term decreasing trend of carbon accumulation. Rates of net increase in above-ground biomass declined by one-third during the past decade compared to the 1990s. This is a consequence of growth rate increases levelling off recently, while biomass mortality persistently increased throughout, leading to a shortening of carbon residence times. Potential drivers for the mortality increase include greater climate variability, and feedbacks of faster growth on mortality, resulting in shortened tree longevity. The observed decline of the Amazon sink diverges markedly from the recent increase in terrestrial carbon uptake at the global scale, and is contrary to expectations based on models.”
In addition, of course, the area covered by rainforest in the Amazon has decreased markedly due to largely illegal logging, reducing even more the forest’s ability to mitigate the effects from ever increasing carbon emissions due to human activities.
Who believes in evolution? Who believes in human-induced climate change?
What do leading figures of the political Right, i.e. the Republicans in the U.S. and the Liberals in Australia, think about important scientific theories? Here are some answers.
EVOLUTION, views of possible Republican candidates for President of the U.S. (a quote from The New Yorker, February 19, 2015: The Evolution Catechism, by Adam Gopnik):
“none of the likely Republican candidates for 2016 seem to be convinced. Former Gov. Jeb Bush of Florida said it should not be taught in schools. Former Gov. Mike Huckabee of Arkansas is an outright skeptic. Senator Ted Cruz of Texas will not talk about it. When asked, in 2001, what he thought of the theory, Gov. Chris Christie of New Jersey said, ‘None of your business.’ ”
http://www.newyorker.com/news/daily-comment/evolution-catechism
HUMAN-INDUCED CLIMATE CHANGE, views of the then opposition leader and now Prime Minister of Australia, Tony Abbott, and the then leader of the Liberals in the Australian Parliament, Nick Minchin (a quote from Klaus Rohde: The Balance of Nature and Human Impact, Cambridge University Press, Cambridge 2013, page 403):
“According to Malcolm Turnbull, a prominent Liberal, the leader of the Australian Liberal party……., Tony Abbott, has publicly declared that man-induced climate change is “crap” (ABC, 2009). Also according to Turnbull, Nick Minchin, the former leader of the Liberals in the Senate, has declared that all the fuss about global warming is nothing but a left-wing conspiracy (ABC, 2009). Lefties who lost their cherished Communist cause now need a new one, and they found it: global warming”.
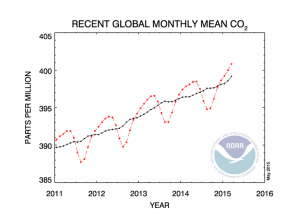








Leave a Reply