Re-imagining geometry

One of the most important powers of mathematics is abstraction. Through abstraction we focus on the essence of a problem.

— Dr Matthew Cooper, Postdoctoral Research Fellow, School of Science and Technology

One of the most important powers of mathematics is abstraction. Through abstraction we focus on the essence of a problem, ignoring extraneous details. One thing we discover again and again is that different-looking problems from science and engineering actually have a common essence. Abstraction then connects knowledge learned from one of these problems to other different problems.” The foci of Dr Matthew Cooper’s current attention are harmonic maps and biharmonic maps, and, he says, this power of mathematics is evident here – what doews this mean for research in mathematics? Let’s re-imagine geometry.

A harmonic map describes the shape of a sheet.

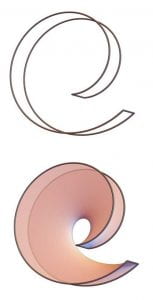
“Imagine you have a thin rubber sheet in the form of a disk. Next, imagine you glue the edges of this to a rigid wire: what overall shape will the sheet take? These concepts are basic in the field of elasticity which plays an important role in engineering with questions such as, “What is the optimal shape of panels on a aircraft?”

“Liquid crystals are an interesting material which have important applications, for example, television and computer screens. You can imagine a liquid crystal screen as a sheet of rod-like molecules, one at each point of your screen. These rod-like molecules point in a particular direction, and they like to align themselves with the molecules close by. Since a direction in three-dimensional space is the same as a point on a sphere, imagine the shape of a globe of the earth; this is the same problem as our rubber sheet from before, but now it must lie on the sphere.”

Here, Dr Cooper says, are two seemingly different problems that are connected through the concept of harmonic maps, and he says, “There are more problems that are connected through this and similar concepts, including one more question relating to biology: Why do red-blood cells take their characteristic biconcave shape? These concepts are also connected to important problems in pure mathematics, such as the Willmore conjecture which asks what is the least bent shape for a doughnut.”¹

Liquid crystals show interesting optical patterns, which are again described by harmonic maps.

Mentors have played an important role in Dr Cooper’s life. “I learned to program at a young age, and all through my early teens I was set on becoming a software developer. Programming was all I thought of.” However, he says, it was the fantastic maths and science teachers in his final years of high school who inspired him to follow a major in Mathematics when entering university. Once at university, inititally he wasn’t really interested in an academic career path. “I had the idea of using my maths and programming skills to make lots of money, perhaps in finance. However, due to the fantastic professors who mentored me, my career aspirations again evolved, and this set me on my current trajectory.”

^{1 Frank Morgan (2012) ‘Math Finds the Best Doughnut’, The Huffington Post, 2 April.
(Accessed: 2 September 2019).}